
宇宙到底有多大?多少岁?
这是仰望星空的人常爱问的两大问题。
但刚开始接触宇宙学的人,很可能遭遇一种困惑:一方面得知宇宙年龄有138亿年,另一方面却被告知宇宙最大直径高达930亿光年,这不是自相矛盾吗?
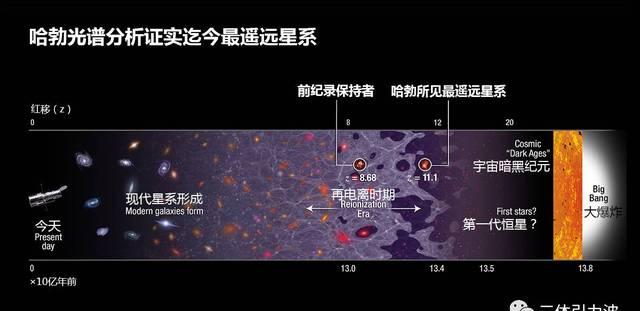
因为按照这些人的理解,从宇宙大爆炸一直到现在138亿年,科学家们一定是找到了确切证据——大爆炸产生的光子,经过漫长的138亿年飞行,终于被我们发现了。(这就像考古学家发现了霸王龙化石,进而确定它们曾生活在6700万~6500万年前一样。)
但,与此同时,科学家又在斩钉截铁地告诉我们:宇宙最大直径竟有930亿光年,也就是说,以地球为中心的可观测宇宙半径有465亿光年。
这么看来,宇宙创世之初——大爆炸最早诞生的光子,飞到现在不是才138亿年吗?为什么科学家竟然会发现465亿光年之外的星体呢?就是说为什么能够发现飞行了465亿年的星光呢?
这不是再明显不过的自相矛盾嘛?!到底科学家集体发昏?还是另有真相?

这的确是个有趣又有料的好问题。科学家告诉我们这两个数据其实没毛病,有毛病的是我们理解有误,以及读书太少。
没耐心刷屏的,一句话告诉你答案,这是宇宙膨胀搞的鬼。
没看懂?那就看一个简单的比喻吧——

想象有一只蚂蚁,爬在一个不断膨胀的气球表面,相对于气球表面的爬行速度是匀速的1cm/s。10秒后,蚂蚁认为自己已经爬了10cm,但旁边的你,作为观测者用尺子测量发现,它爬过的这段距离已经超过了10cm,因为气球在膨胀!同样道理,代表宇宙年龄的光子,尽管飞行时间是138亿年,却能够跨过465亿光年。都是因为宇宙膨胀造成的!懂了吧。

但问题来了,这不是大大超过了光速吗?传说中的超光速真实存在吗?宇宙年龄和大小到底是怎样测量出来的?宇宙膨胀又是怎么测量的?
有耐心想知道「知其所以然」的,请看——
先来说说宇宙年龄。
事实上,测定宇宙年龄,并不是像有人想当然的那样,跟发现霸王龙化石一样,科学家找到了宇宙大爆炸的最初影像资料。
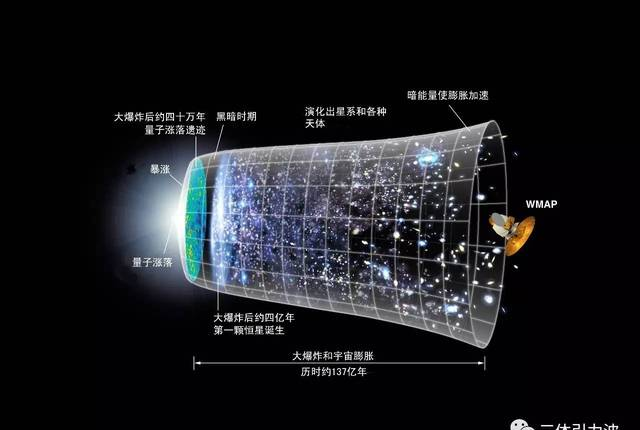
按照大爆炸理论,这是不可能的。因为从宇宙大爆炸开始,大概30万年后,宇宙最早一批原子才开始诞生;大概35万年(也有称38万年的),光子才开始在宇宙中向四面八方传播,此时整个宇宙直径只有1亿光年。

这些最初的光子,一路飞越到现在,就是我们今天探测到的宇宙微波背景辐射,简称CMBR。可以说是宇宙大爆炸的余波,也可以说是「宇宙的第一束光」或者「婴儿宇宙快照」。
这样的话,只要测得CMBR越精确,确定的宇宙年龄也就越接近。
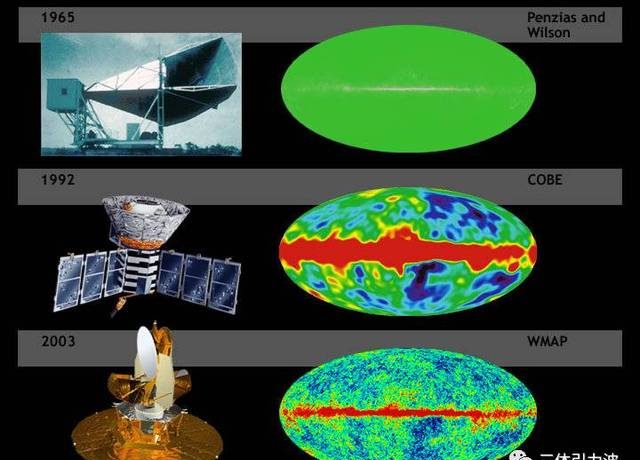
从最早美国两位工程师通过射电望远镜——意外发现,到1992年NASA发射宇宙背景探测者(COBE)——主动探测,再到2003年NASA发射第二代宇宙微波背景探测器(WMAP)和2009年欧空局ESA发射普朗克卫星——深度探测,再加上哈勃太空望远镜和一大波地面天文台的数据共享/互补对照……经过半个世纪的不断努力,最新测定的宇宙年龄——137.98±0.37亿年,一般简化成138亿年。

再说说宇宙大小。
通常说的930亿光年,是指可观测宇宙的直径。
什么又是可观测宇宙?简单来说,就是以观测者为中心所能观测到的宇宙范围。言外之意,可观测宇宙只是整个大宇宙的一部分。从宇宙大尺度来说,不同观测者的可观测宇宙范围也不同。
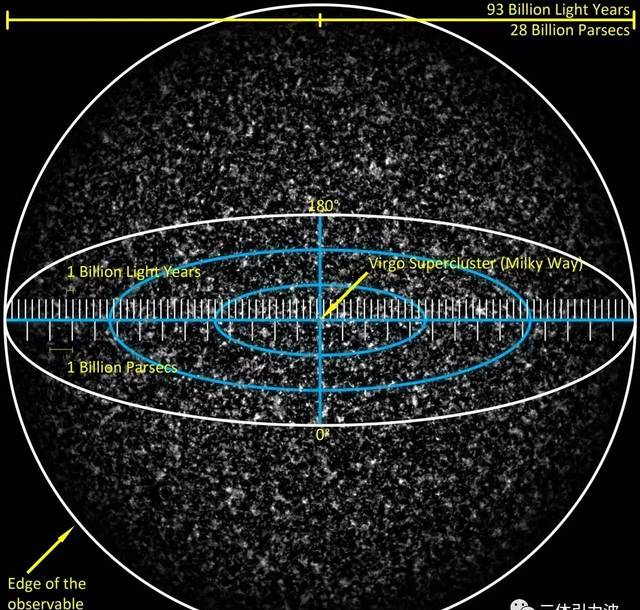
以我们为例,人类目前的可观测宇宙其实是个球体——一个以465亿光年为半径的巨巨巨型球体。
球体外面是什么?可观测宇宙之外是什么?其实还是大宇宙的一部分,只不过是我们还没能力观测到。
目前已知的这个半径又是怎么来的?
其实,并不是我们观测到了距离地球465亿光年之外的星体。

▲目前为止人类观测最远的星系——GN-z11,根据哈勃望远镜的测定,它的年龄高达134亿年,距离我们大约320亿光年。此处——又一个年龄与距离高度不符,到底咋回事?等下你就懂了。
测量可观测宇宙半径465亿光年,其实,我们还是根据测定CMBR——宇宙微波背景辐射——粒子的红移量,得到了共动距离,大约是465亿光年,这就是可观测宇宙半径。
等等,红移量、共动距离又是什么?

先说距离,宇宙学中经常使用的有三种距离:光行距离、固有距离、共动距离。
光行距离最为我们大众所理解,就是用光飞行的时间来衡量距离。光行距离有一个前提就是不考虑宇宙膨胀。为了使用方便,光行距离派生出「光行时间」——光行这段距离所需的时间,有时也被称为「回溯时间」。事实上,宇宙年龄138亿年,也可以说是光行时,或者说回溯时间是138亿年。

再比如,我们说牛郎织女星相距16光年,也就是指它们之间的距离需要光飞行16年,光行距离16光年,光行时/回溯时间16年。
但如果考虑宇宙膨胀,前面说过的观测到最远星系——距离我们320亿光年,事实上就没那么简单了。因为在光行320亿年的这段时间里,整个宇宙是在不停地膨胀。所以,要想测定星体的真实距离,还需要考虑宇宙在这么长的时间里到底膨胀了多少?

再简单说下,宇宙膨胀——这是从大爆炸开始就从未消停地「宇宙大动作」。最早被大名鼎鼎的哈勃发现,建立了宇宙膨胀理论,形成了哈勃定律、哈勃常数、退行速率、红移量等等。如今已成为宇宙学最热门的研究领域之一,因为它决定了很多重要命题。在这里,你只要能理解这个比喻就好——

宇宙膨胀的道理,就像葡萄干面包一样,放进烤箱里烘烤时,面包会从小变大的膨胀,不管是面包表面还是里面的葡萄干,在这个膨胀过程里,都会相互远离。
现在,科学家对宇宙的观测结果正好与此吻合,所有星系都在远离我们!葡萄干都在相互远离!科学家把这种远离我们的宇宙膨胀速度,也叫退行速度,相对我们来说这些星系都在退行。
又因为这个速度是根据光谱红移现象测量的,所以引入一个「红移」概念。这个我们后面再说。

我们有了宇宙膨胀的概念后,你就能理解「共动距离」了。共动距离的「共动」,到底是谁跟谁共动?
其实是测量宇宙距离的量天尺,跟宇宙膨胀一起共动——共同膨胀。这种想象出来的量天尺,测量出的距离就是共动距离,也有叫同移距离的。这就意味着,测出来的仍是膨胀前的数值,所以,共动距离是一个固定值。
可观测宇宙半径为465亿光年,就属于共动距离。为什么此处要采用共动距离呢?

其实,这正是科学的严谨说法。你想想,宇宙时时刻刻都在加速膨胀,而且膨胀速度很惊人,越来越多的星系在远离我们,最终变成不可观测。所以,对于这种动态的宇宙来说,最妥当的说法就是采用共动距离——这个固定值,描述可观测宇宙的尺度,和宇宙一起膨胀,不随时间变化,更适合描述这个加速膨胀的宇宙大小——半径465亿光年的巨型球体。
跟共动距离概念——正好相反的是「固有距离」,一种随宇宙膨胀而变化的距离,相当于使用一把固定不变的量天尺,去测量膨胀中的宇宙距离。也就是说,这是一个随时间变化而变化的数值,当然这是一个理想值。
尽管固有距离实际上无法测量,但在科学家眼里却是一种最接近真实距离的概念。于是,科学家找到一种替代方案,这就是红移量。
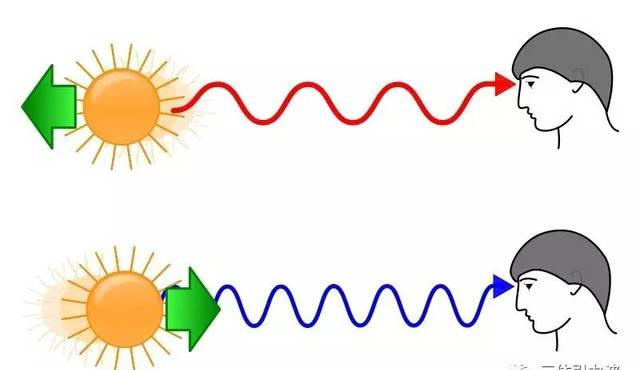
所谓红移,就是光子辐射的波长,随着宇宙膨胀会被拉长,从光谱蓝色的短波移动到红色的长波,因而形成了红移现象。
红移是一个很直接的量,因为直接观测,就能得出数值。
一束光的红移,就是遥远星光的观测波长—真实波长,再与真实波长的比值。


▲图右是遥远的星系在可见光波段的光谱,与图左太阳的光谱比较,可以看见谱线)朝红色的方向移动,即波长增加(频率降低)。
请记住,红移量是我们谈论宇宙尺度、星体距离时,唯一能够明确的测量值,而其它比如光行距离、共动距离、回溯时间,都是派生出来的量。至于这些量之间是如何换算的,要涉及到一堆数学公式,还是就此略过。
对我们来说,最简单最有用的就是一张对照表——回溯时间、光行距离、共动距离、红移量、膨胀速度之间关系的对照表,足够用了。

我们可以很清晰查到:当宇宙年龄是138亿年(回溯时间)时,所对应的共动距离是465亿光年,红移量是100。
再比如,最远星系GN-z11的回溯时间,即星系年龄134亿年,对应的共动距离就是320亿光年。而这些数值也都是通过测量——从这个星系发出光子的红移量换算出来的。
我们懂得了回溯时间、共动距离、红移量之间的关系,是不是一下子豁然开朗了不少?

最关键的问题来了:宇宙回溯时间/光行时间是138亿年,共动距离却是465亿光年,这不是大大超过了光速吗?不是正好说明因宇宙膨胀造成的超光速现象吗?
可以肯定的是,我们还没有发现任何「超光速的光」。光的最高限速还是30万公里/小时,无法自我突破或者借助外力超越。
至于说,宇宙第一束光——宇宙微波背景辐射,在138亿年里跨越了465亿光年,大大超过了137亿年的光行距离。读懂上面我所说的,其实就该弄懂了——绝不是宇宙第一束光超越了光速,而是宇宙加速膨胀使得第一束光看起来好像超光速,这不过是我们作为观测者,看到的一种观察效应。

细心的人从上面那张表也会发现,第二栏v/c退行速度与光速比值最大就是1,不管现在还是未来,都没有大于1,并不存在超光速的现象。

这就像我上面列举「蚂蚁爬气球」的栗子,蚂蚁还是以自己的速度爬行,但在气球膨胀作用下,观测者却测出了大大超过蚂蚁的爬行速度和爬行距离。但是,我们并不能就此得出结论:这只蚂蚁变成了超级蚂蚁,竟然超越了蚂蚁界的最高速度。

总之,我们大可不必担心/期望可观测宇宙存在超光速的光,作为本宇宙的最快信使——光信使已经是最高限了,这是由宇宙法则决定的。
1.《为什么宇宙年龄138亿年,大小竟有930亿光年?》援引自互联网,旨在传递更多网络信息知识,仅代表作者本人观点,与本网站无关,侵删请联系页脚下方联系方式。
2.《为什么宇宙年龄138亿年,大小竟有930亿光年?》仅供读者参考,本网站未对该内容进行证实,对其原创性、真实性、完整性、及时性不作任何保证。
3.文章转载时请保留本站内容来源地址,https://www.lu-xu.com/caijing/7303.html