过程能力指数和过程性能指数的深度解析

当我们在收集过程的数据时，会有如下疑问，这个过程产生不良的风险是多少？要回答这个问题，需要 进行“过程能力分析”。过程能力分析的基本思想，就是将“顾客之声”与过程之声相比较。

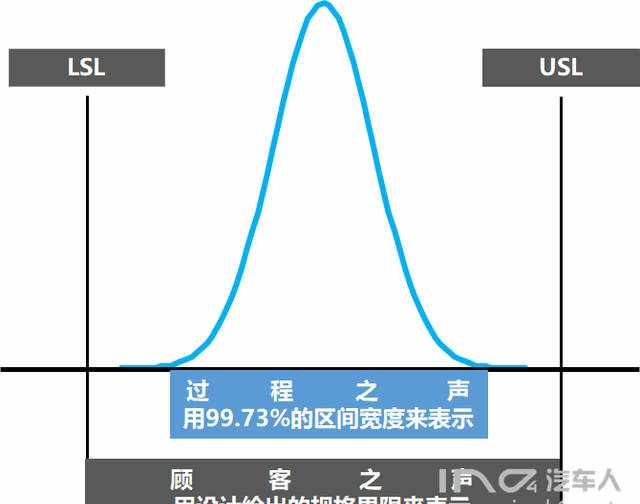
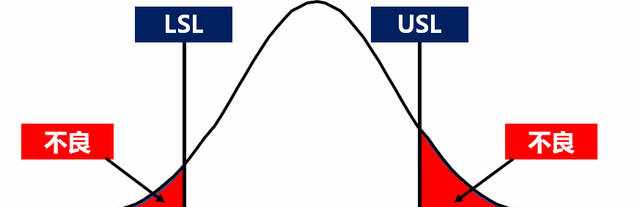
根据过程能力，可以评估“超出规格界限的比率”是多少？

有时，测量系统是计数型的，也即是说，只能获得合格/不合格的结果。这个时候无法得到具体读数，而只能获得不良率结果，比如PPM。有一种观点认为，可以通过查表将PPM转化为西格玛水平来体现计数型数据的过程能力。但是，这种分析需要一些前提假定。

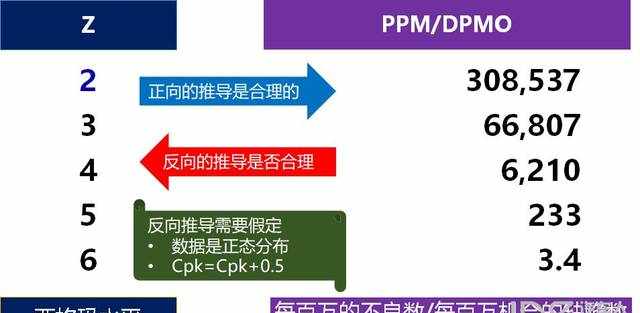
而且，这种转换并没有很大的现实意义，因为……

因此，我们通常只对计量型数据进行过程能力分析。在之前的文章中，我们提到，计算过程能力指数Cp/Cpk和过程性能指数Pp/Ppk有一些前提要求。

那么，为什么过程能力指数Cp/Cpk需要四个前提，而过程能力指数只需要二个前提呢？我们来逐条分析。

【MSA】前提

两者都需要测量系统分析满足要求，这个是容易理解的，因为只有测量读数是有效的，才能计算出正确的能力指数。

【数据独立】前提

两者都需要数据独立，数据不独立会影响变异的估计。具体的介绍见时间序列分析的相关内容。不过，在机械制造行业，如果抽样是随机的并且抽样间隔是合适的（间隔时间不是特别短），可以不必进行独立性是否满足要求的假设检验。

【过程稳定】前提

这是过程能力指数Cp/Cpk的要求，但是过程性能指数Pp/Ppk并不需要满足这个要求。原因在于，虽然两者的公式看起来都一样，但是对于变异（总体标准差σ）的估计方式是不同的。

过程能力指数Cp/Cpk只评估组内变异。下面是Minitab软件对Cp/Cpk公式中，在正态分布的前提下，总体标准差σ的估计方式。

我们发现，无论是“子组极差的平均值”的估计方法、还是“子组标准差平均值”的估计方法、或是”合并子组标准差“的估计方法，它们都只是考虑了每个子组（本身）的组内变异，没有考虑子组之间的变异。

那么，为什么不考虑子组之间的变异？因为，Cp/Cpk的计算是要求先进行过程的稳定的评价。即，在休哈特控制图中没有发现异常点。满足这个前提之后，在统计层面可以认为：子组之间的组间差异是（统计层面的）“0”，所以只需要考虑组内的变异即可。这就是一定要先做常规控制图，判稳之后才能计算Cp/Cpk的原因。

那么，Pp/Ppk为什么不需要过程稳定就能计算了呢？因为Pp/Ppk是基于整体变异。在正态分布前提下，总体标准差σ的估计方式如下。

80%

1

步