世界最简易的公式计算

严格意义上来说，人们全部文明行为非常大都创设在数学课上。而基本上全部公式、繁杂的基础理论都创设在世界最简易的公式计算上，1 1=2。这一看起来简易却高深莫测的公式是怎么来的？在历史上的一位数学家会怎么解释1加1为何相当于2？

发觉世界最简易的公式计算1 1=2，代表着哪些？

这一连三岁小孩都能立懂的公式计算是人类发展史问世的起始点，它充分说明着自然数的问世，引起不断几千年的数据爆发。数学课创生的所有基础公理都蕴涵在其中。

而它到底究竟是从哪里而来的呢？，又将推动人们向何而去？

人生道路认字忧虑始，人们的全部苦恼，也是否由于知道1 1=2呢？

人们刚开始注意到数学课的能加性

早在远古时期，大家的老祖先就在贮藏猎食、分派食材时，慢慢造成多数的觉得。

当2只牛、3只羊、5只猪摆放在一块，仅有这种物品可越冬时，明显的求生欲使老祖先若隐若现地意识到这在其中有一种关联性，并刚开始摆布着自身仅有的10只手指头记数。殊不知，从这类初始的抽象性觉得到实际的数的概念的产生，却经历了极为悠长的历史时间时光。

因而，当一位古时候祖先第一个意识到1 1=2，进而了解到两个数求和获得另一个明确的数时，就发觉了数学课一个十分关键的特性——能加性，它是人类发展史上一个极为杰出的時刻。

好似钻木取火，1 1=2的最开始应用也仅是不得已地为了更好地存活，二者一样最少拥有 三十万年的历史时间，创造美好生活，但自然数的产生却远比火的问世有深刻影响。

1 1=2，有关这一公式计算，最形象化牵涉到的便是自然数和加减法。

大家早已没法资格证书，加减法到底是在什么时候被人们创造发明的，由于沒有充足详尽的参考文献纪录，乃至很有可能沒有文本。但加减法的出現，毫无疑问是为了更好地在互换产品或战俘时开展计算。

＋、－与自然数的出現

听说，那时候红酒商在卖出喝醉酒，曾用水平线标明桶里的储存，而当桶里的酒又提升时，便用竖线框把原先画的水平线划去，因此就出現用于表明降低的－和用于表明提升的＋。最终直至1630年，＋做为运算符号才获得大伙儿的认可。

而有关自然数的出現，却比＋、－刚开始地更早，大概在一万年之前，冰川褪去了。石器时代M，这些马背的游牧人狙击兵，在中东地区的山内悄悄的开始了一种更好的生活。她们革除掉凶横捕杀的天性，刚开始老老实实田边，栽种，开展农作，这时候，怎样纪录时间、时节，如何计算个人收藏谷类数、种子数可为难住了这群四肢发达的壮男。

特别是在白尼罗河谷、底格里斯河与幼发拉底河河段，还发展趋势起了更繁杂的农业社会，这群刚进入新时代的农户还碰到了缴纳租税的难题。显而易见，以往石器部落文化艺术里汇总的一、二、三、多已还不够用了，大家急需解决数有名字，并且记数务必更精确些。

殊不知，没人见过自然数，也没人了解它是怎么排序遍布的。

它是用于计量检定事情的产品数量或表明事情顺序的数，它的遍布也许是跌跌撞撞一个圈，也许是螺旋式交叠缠绕式，也许是放射性发生爆炸散发式的，不一样挑选便会有不一样的数学世界。但最后数学世界最终挑选的是1、2、3、4、5……那样一个不可逆的直线型的井然有序管理体系。

图1-1

皮亚诺如何使用五个基础理论长出：1 1=2

大家都了解1 1=2，但你是不是有想过为何1 1就相当于2呢？

这个问题，没去思索还行，一思索如同鸡生蛋還是蛋生鸡这一难点一样，会将你绕得恍恍惚惚，好在都会有那麼几个具备哲学思维的一位数学家爱不辞劳苦地去思索、证实它。

而在这里在其中，西班牙一位数学家皮亚诺用基础理论把自然数放置在了数学世界里边，用五条公理创建了一阶算数系统软件，能够用于计算出1 1=2这一数学世界的起点。

基础理论一：0是自然数。

一望无际的数学课宇宙空间里，如下图所示，此后拥有第一个影子存有——0。

图1-2

基础理论二：每一个明确的自然数a，都是有一个明确的后续数a’，a’也是自然数。

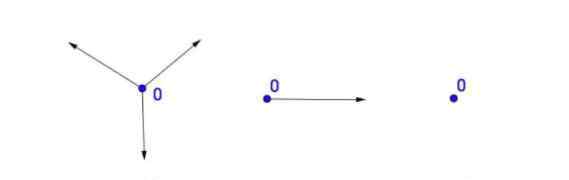
那麼，这一自然数起始点0是如何暴发的呢？后续守候者会以哪些的方式出現？顽皮地围住0四处散发，或者悄悄地跑到0的后边，亦或是绝情地留0一数量在哪？

基础理论二作出了挑选，让诺大的数学课室内空间中，出現的每一个数都有着着一个明确的后续数陪着我自身，如图所示：

图1-3

基础理论三：0并不是一切自然数的后续数。

为了更好地防止后继者不讲规矩跑到0的旁边，公理3明确了0务必也只有是自然数的第一个数。可是束手无策，这群后继者很有可能也没那麼安分守己，她们还很有可能由于同一个女孩吵嘴。换句话说，有可能3的后续数3′=3，也很有可能2的后续数2′=3。如下图1-4，出現这类状况：

图1-4：不一样的自然数有不一样的后续数。

基础理论四：为防止上述所说情况，公理4连忙着出去界定，假如n与m均为自然数且n≠m，那麼n’≠m’；假如b、c均为自然数，且b’=c’，那麼b=c；同一个自然数的后续数相同，不一样自然数的后续数不相同，那样，3就不太可能即是2的后续数，也是3的后续数了。但假如出現图中2.5那样的数呢？

图1-5

为了更好地祛除2.5那样非自然数的出現，基础理论五出現了。

基础理论五：假设P（n）是自然数的一个特性，假如P（0）是对的，且假设P（n）是恰当的，则P（n’）也是确实，那麼出题对全部自然数都为真。

它也有此外一种方式：设S是自然数集的一个非空子集，且考虑（i）0归属于S；（ii）假如n归属于S，那麼n’也归属于S；则S是包括全体人员自然数的结合，即S=N。

这儿的叫法很有可能会有点儿绕，阅读者很有可能并不是很了解。实际细剖，它是数学中的归纳公理，换句话说假如有一个自然数的特性，那麼全部自然数都将考虑这一特性，不符合的就并不是自然数。那样，我们可以界定自然数系：存有一个自然数系N，称其原素为自然数，当且仅当这种原素考虑基础理论一至五。

再界定加减法是考虑下列二种标准的计算：

1.针对随意自然数m，0 m=m；

2.针对随意自然数m和n，n’ m=(n m)’。

那样，大家就可以证实1 1=2：

1 1=0′ 1=(0 1)’=1′=2；

或是，1 1=0′ 0′=0”=2。

或是，由于1 1的后续数是1的后续数的后续数，即3；又由于2的后续数也是3，依据皮亚诺基础理论4，不一样自然数的后续数不一样，因此 1 1=2。

那样，依据皮亚诺五个基础理论创建起來的皮亚诺一阶算数系统软件，大家就计算出了1 1=2。

用哥德巴赫猜想计算1 1=2

另一个（1 1）

计算出1 1为何相当于2，并不可以刁难这些脑路清楚，异于常人的一位数学家们。怎么解决人世间另一个1 1，这才算是这群一位数学家的心头疼。

哥德巴赫猜想，是数学课黄冠上一颗可望而不可即的耀眼明珠，称得上全球近现代三大数学难题之一。

大约在18世纪上下，法国一富二代哥德巴赫，厌烦锦衣玉食的日常生活，不管不顾亲人阻止，硬要跑去一名中学老师，还此后一发一发不可收拾地爱上数学，就连夜里回家了歇息，也在倒腾着阿拉伯数。而他平生最爱玩的游戏竟然加法运算，并且仍在玩加减法手机游戏的全过程中发觉了一个奥秘：一切超过5的合数全是三个素数之和。

但令他无可奈何的是，他越玩越不成功，如何也没办法证明自身的发觉。之后，只有有求于那时候数学界的权威性达人欧拉。

1742年6月7日，哥德巴赫写信欧拉，明确提出：一切超过5的合数全是三个素数之和。随意取个合数77，可写出三个素数之和，77=53 17 7；再任取一个合数461，461=449 7 5，也是三个素数之和，461还能够写出257 199 5，依然是三个素数之和。

想不到独眼巨人欧拉竟然也被这个问题给刁难住了，1742年6月30日，欧拉给哥德巴赫复信：这一出题看来是恰当的，可是他也给出不来严苛的证实。为了更好地挽留下自身竟然也给出不来证实的情面，奸诈的欧拉另外还明确提出了另一个等价命题：一切一个超过2的双数全是2个素数之和。但这一出题他也没能给与出证实。

而那样一个任一充足大的双数，都能够表明变成一个素因子数量不超过a个的数，与另一个素因子不超过b个的数之和出题，就被统记作a b，哥德巴赫猜想（也称哥德巴赫–欧拉猜想），也就被称作另一个（1 1）。

1、0的奇妙奥秘

在法国图灵根着名的郭塔皇宫公共图书馆，有一份难能可贵的稿件，它的题目为：

1与0，一切数据的奇妙历史渊源。它是创造物的密秘美好的楷模，由于，一切只不过都来源于造物主。

它是法国超级天才高手莱布尼茨的手迹，它用两页出现异常精练的叙述，创造发明了一个奇妙美好的数据系统软件——二进制，他告知大家，1 1≠2，在电脑代码全球里，1 1=10。

二进制是建筑科学中普遍选用的一种数制。二进制数据信息是用0和12个数码来表明的数。它的数量为2，进位标准是逢二进一，借位标准是借一当二。当今的电脑操作系统应用的大部分便是二进制系统软件，数据信息在电脑上中主要是以补码的方式储存的。

可以说，从二十世纪第三次信息革命暴发至今，人们就刚开始进入了电脑上时期，我们在虚似的互联网里手机游戏、社交媒体、欢乐。到现在二十一世纪，刚开始着眼于人工智能技术的开发设计，而这种物品实质上全是由电脑上完成的。

而将来，彻底身处在数字时代的大家，终将被二进位程序流程码全身上下笼罩着，这世界，1 1就只很有可能相当于2吗？

无论是现实生活中简要通俗易懂的1 1=2，或者数论全球里让人煞费苦心的1 1，還是虚幻世界里的1 1=10，都以其本身的普遍性和普遍意义在時间的时光里不证自明，让人们能以其为始，在接纳这种公式计算和定律的标准下，再次用客观的方式计算衍化出天地万物。并在天地万物中，能随便地偷窥其足迹。

招架不住的腾讯王者荣耀是由0和1的程序流程码写运作；

放置iPhone的天秤座则彻底考虑能加性的量；

总品质一直相当于每一个物体的质量之和；

1 1=2扛起了人们客观全球的基础运行，超越人类发展史自始至终，不用名字，不用汉语翻译，也不用表述。

它无所不在，藏匿于天地间，自身就有着着流连忘返的艺术美。