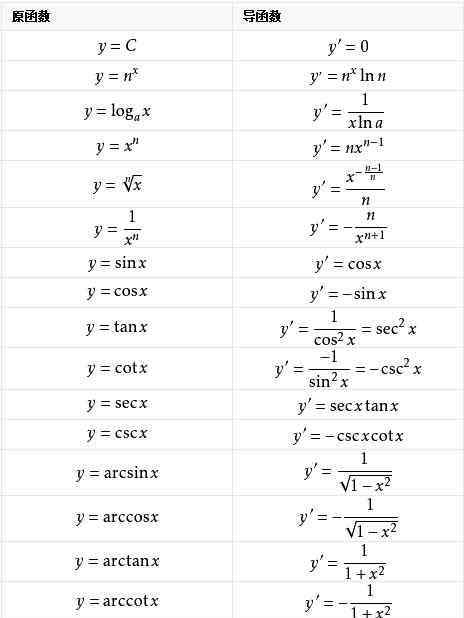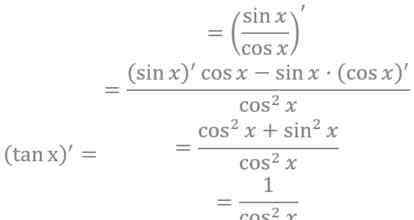指数函数的求导公式:(a^x)"=(lna)(a^x),实质上,求导就是一个求极限的过程,导数的四则运算法则也来源于极限的四则运算法则。反之,已知导函数也可以倒过来求原来的函数,即不定积分。

指数函数的求导公式:(a^x)"=(lna)(a^x)
求导证明:
y=a^x
两边同时取对数,得:lny=xlna
两边同时对x求导数,得:y"/y=lna
所以y"=ylna=a^xlna,得证
对于可导的函数f(x),x↦f"(x)也是一个函数,称作f(x)的导函数(简称导数)。寻找已知的函数在某点的导数或其导函数的过程称为求导。实质上,求导就是一个求极限的过程,导数的四则运算法则也来源于极限的四则运算法则。反之,已知导函数也可以倒过来求原来的函数,即不定积分。
导数的求导法则1、求导的线性:对函数的线性组合求导,等于先对其中每个部分求导后再取线性组合。
2、两个函数的乘积的导函数:一导乘二+一乘二导。
3、两个函数的商的导函数也是一个分式:(子导乘母-子乘母导)除以母平方。
4、如果有复合函数,则用链式法则求导。
部分导数公式1.y=c(c为常数) y"=0
2.y=x^n y"=nx^(n-1)
3.y=a^x;y"=a^xlna;y=e^x y"=e^x
4.y=logax y"=logae/x;y=lnx y"=1/x
5.y=sinx y"=cosx
6.y=cosx y"=-sinx
7.y=tanx y"=1/cos^2x
8.y=cotx y"=-1/sin^2x
1.《a的x次方的导数 a的x次方的导数》援引自互联网,旨在传递更多网络信息知识,仅代表作者本人观点,与本网站无关,侵删请联系页脚下方联系方式。
2.《a的x次方的导数 a的x次方的导数》仅供读者参考,本网站未对该内容进行证实,对其原创性、真实性、完整性、及时性不作任何保证。
3.文章转载时请保留本站内容来源地址,https://www.lu-xu.com/jiaoyu/433109.html