如果同一平面内的四个点在同一个圆上,则称这四个点共圆,一般简称为“四点共圆”。共圆的四个点所连成同侧共底的两个三角形的顶角相等。

四点共圆怎么判定
判定1
从被证共圆的四点中先选出三点作一圆,然后证另一点也在这个圆周上,若能证明这一点,即可肯定这四点共圆.
推论:证被证共圆的点到某一定点的距离都相等,从而确定它们共圆.即连成的四边形三边中垂线有交点,可肯定这四点共圆.
判定2
1:把被证共圆的四个点连成共底边的两个三角形,且两三角形都在这底边的同侧,若能证明其顶角相等(同弧所对的圆周角相等),从而即可肯定这四点共圆.
2:把被证共圆的四点连成四边形,若能证明其对角互补或能证明其一个外角等于其邻补角的内对角时,即可肯定这四点共圆。
判定3
把被证共圆的四点两两连成相交的两条线段,若能证明它们各自被交点分成的两线段之积相等,即可肯定这四点共圆(相交弦定理的逆定理);或把被证共圆的四点两两连结并延长相交的两线段,若能证明自交点至一线段两个端点所成的两线段之积等于自交点至另一线段两端点所成的两线段之积,即可肯定这四点也共圆.(割线定理的逆定理)
判定4
四边形ABCD中,若有AB*CD+AD*BC=AC*BD,即两对边乘积之和等于对角线乘积,则ABCD四点共圆。该方法可以由托勒密定理逆定理得到。
托勒密定理逆定理:对于任意一个凸四边形ABCD,总有AB*CD+AD*BC≥AC*BD,等号成立的条件是ABCD四点共圆。
判定5
西姆松定理逆定理:若一点在一三角形三边上的射影共线,则该点在三角形外接圆上。
四点共圆性质
若A、B、C、D四点共圆,圆心为O,延长AB至E,AC、BD交于P
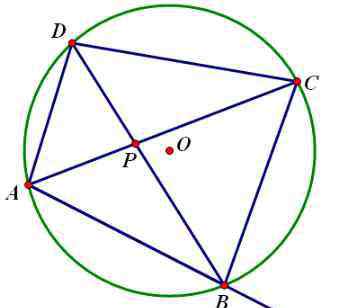
性质一:∠A+∠C=180°,∠B+∠D=180°
性质二:∠ABC=∠ADC(同弧所对的圆周角相等)
性质三:∠CBE=∠D(外角等于内对角)
性质四:△ABP∽△DCP(三个内角对应相等)
性质五:AP×CP=BP×DP(相交弦定理)
性质六:AB×CD+AD×CB=AC×BD(托勒密定理)
1.《四点共圆的性质 四点共圆的判定方法都有哪些》援引自互联网,旨在传递更多网络信息知识,仅代表作者本人观点,与本网站无关,侵删请联系页脚下方联系方式。
2.《四点共圆的性质 四点共圆的判定方法都有哪些》仅供读者参考,本网站未对该内容进行证实,对其原创性、真实性、完整性、及时性不作任何保证。
3.文章转载时请保留本站内容来源地址,https://www.lu-xu.com/jiaoyu/442409.html









