失踪的正方形 骗人的数学题，那消失的1块钱到底被谁拿走了

1、缺失的方块

这个谜题是美国业余魔术师保罗·加里在1953年发明的，所以也被称为“加里悖论”，所有像加里悖论这样的谜题都被称为“剪裁悖论”。

当你在农历正月初一看这个动画的时候，你会觉得这个小广场简直消失的没有一点瑕疵。

然后，如果你仔细看，你会发现两个“三角形”的大小是不一样的，只是给我们造成了一种视觉上的错觉！

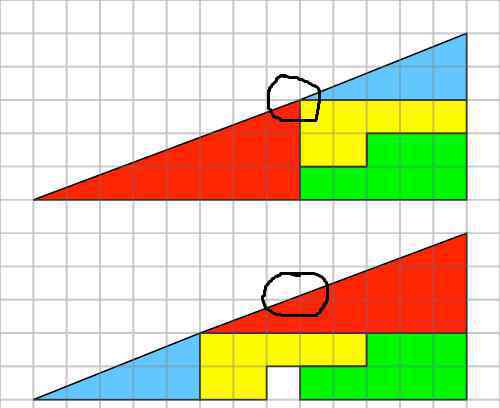
“缺失的正方形”被指定为斜边

2.斑马问题

这个谜题的所有条件包括:

房屋颜色:红色、绿色、白色、蓝色和黄色

国籍:英国、西班牙、日本、意大利、挪威

工作:画家、摄影师、外交官、小提琴手和医生

饮料:茶、牛奶、咖啡、橙汁、矿泉水

宠物:狗、蜗牛、狐狸、马和斑马

1.一条街上有五栋不同颜色的房子。每栋房子都住着不同国籍的人。每个人都有不同的职业，喝不同的饮料，养不同的宠物。

2.英国人住在红色的房子里；

3.西班牙人有一只狗；

4.日本人是画家；

5.意大利人喜欢喝茶；

6.挪威人住在左边第一栋房子里；

7.绿房子在白宫的右边；

8.摄影师养了一只蜗牛；

9.外交官住黄房子；

10.中间房子的那个人喜欢喝牛奶。

11.喜欢喝咖啡的人住在绿色的房子里；

12.挪威人住在蓝房子旁边；

13.小提琴手喜欢喝橙汁；

14.养狐人住的房子和医生家相邻；

15.马主住的房子和外交官的房子相邻。

那么，谁喝水，谁的宠物是斑马呢？

其实这个复杂的谜题有无数个版本。传闻爱因斯坦小时候编的。有人说作者是刘易斯·卡罗尔。

既然不可能找出是谁创造了这么有趣的问题，那就来看看答案是什么。。。

3.新西兰面试问题

京西宾馆准备住3个人，每人每晚需要10元，一共30元。于是哮天向他们每人收了10元钱。

后来刘老板心情很好，想给他们一些优惠，就对哮天说:今天的优惠够25块钱了，你把5块钱还给他们吧。

哮天想:5块钱怎么还给三个人？既然强西老板今天这么高兴，奖励我2块钱就可以了。。

于是，哮天收了2元钱，然后把3元钱还给三位乘客。

一切看似正常，但请看以下计算:

刚开始每人出10元，现在退回到1元，也就是10-1=9，每人只花了9元钱，三个人每人花了9元，3 X 9 = 27元+2元=29元。。。

还有1块钱，钱去哪了？？？

当你有了这个想法，就说明你被绕过了。。。

其实等式27+2 = 29本身就是错的！

27元里包含了手里的2元，27-2 = 25是刘手里的钱，不算少。

关于这个故事，有网友写了一个后续，找到了所谓的“失落的美元”。

几个月后，两名乘客再次入住京西宾馆，哮天每人得到10元，共计20元。

后来刘老板想给乘客优惠，也是优惠5块钱；然后是哮天，他私下里保留了3元钱，给每个乘客1元钱。

现在每位乘客交了9元钱，加起来是18元，加上哮天手里的3元钱，总共是21元。

看，少的1块钱在这里！

4.海盗黄金拼图

这是博弈论中的经典问题，这个谜题的描述也是一个有趣的故事:

有A、B、C、D、E五个海盗，抢了100个金币，现在要分赃。

海盗世界等级分明，这五个海盗排名如下:a > b > c > d > e。

分享赃物的制度也很民主:首先是等级最高的海盗提出分配方案，然后所有海盗投票接受。如果半数以上的人同意，提案就通过；否则，提议者会被扔进海里喂鲨鱼，排名第二的海盗会提议，以此类推。。。

假设“每个海盗都极其聪明理性”，那么“第一个海盗提出什么样的分配方案来最大化自己的收益？”

从后到前，首先要知道D提出的方案绝对是最终方案，因为不管E同意与否都可以通过，所以D和E都不用担心被抛入海中。当时e得0金币，d得100金币。

e:因为D提出方案的时候，他的金币是0。所以只要D之前的人分配的金币大于0，就同意方案。

d:如果C提出的方案肯定能通过，那么自己获得的金币就是0，那么只要B允许自己获得的金币大于0，就同意了。

c:因为你自己想出方案就可以给E一个金币，你自己的方案就通过了，但是考虑到B自己想出方案就给D一个金币，B的方案就通过了，你得到的金币是0。所以，只要A让自己拿到0多金币，他就会同意。

b:因为当你想出自己的方案时，只需要给D一枚金币，就可以通过了。不需要考虑C和E是否同意，所以无论A怎么提出，你都不会同意。

甲:乙肯定不会同意的。但是只要给C一枚金币，E就可以传一枚金币。

所以对于A来说，最好的方案是:A得98金币，B得0金币，C得1金币，D得0金币，E得1金币。

这个答案极其出人意料。

总的来说，我们都认为金币应该分给其他四个海盗，让他们通过求婚来保命，但最终的答案告诉我们，贪婪更好。。。

5.无法完成的谜题

这个“不可能的谜题”的描述如下:

有两个不相等的整数x和y，都大于1小于100。数学家“何先生”知道这两个数的和，数学家“积先生”知道这两个数的积。他们有如下对话:

吉先生:我不知道X和Y是什么。

先生:我知道你不知道。

吉:我现在知道了。

何先生:你知道，我也知道

那么，x和y是什么？

已知条件如此之少，难怪被称为“不可能的谜题”！

图灵奖得主阿兹埃尔·迪杰斯特拉(Azhel Dijiestra)曾说过，他曾多次试图用心算来解决这个问题，但多次都睡着了。最后，在一个不眠之夜，他花了六个小时没有用纸和笔在脑子里解决问题。

看完之后。。。

脑子好。使用。很多。就是这样。