起数学思想的难题

微信发朋友圈有朋友问起数学思想的难题，今日详尽谈一谈.

流行的叫法，数学思想有四大：函数与方程观念、分类讨论观念、数学思想观念、化归与转化思想.

咦，仿佛哪些行业都是有四大？

四大名捕，四大天王，四大会计师公司，四大名著......额，很有可能四个易记吧.

一、函数与方程观念

在提到了涵数观念，方程思想和它算作好基友吧.

1.是否想起把给出的式子当做有关某一未知量的方程组，是否想起科学研究这一方程组根的状况.

看一个板栗.

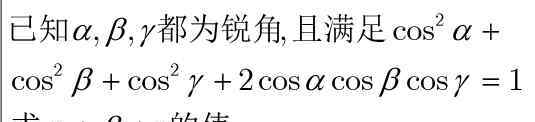
剖析：已经知道和所愿差别非常大，化简方位未知，求得较艰难.如果我们换一个逻辑思维视角，把标准当作有关某一自变量的二次方程，也许能简单化计算.

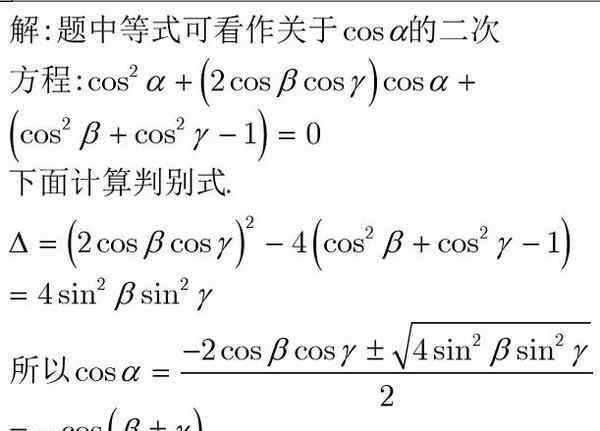
自然，相信根据形变、化简也可以获得上边的結果，可是不如这样解决来的立即，条理清晰.

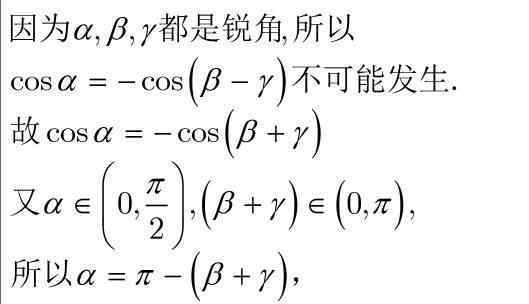
2.求得n个未知量时是不是想起找寻n个单独的方程组？

这也是方程思想的一般反映.

特别是在在圆锥曲线大题中，方程思想反映的酣畅淋漓.

圆锥曲线大题的特性便是几何图形量多，量中间的关联盘根错节.有些人说解析几何便是托关系，道出了关键所属.

在这类状况下，大家期待先后、逐渐地把各几何图形量求得解决是不太好完成的.秘诀便是创建有关他们的方程组，要解好多个未知量就需要创建好多个方程组.

二、分类讨论观念

分类讨论观念又分成归类与融合观念.即先对繁杂的状况开展归类，随后把各一部分的結果融合在一起.

在日常生活中，大伙儿有那样的感受，有些人询问你一个很含糊的难题，你没法得出确立的回答.

例如，有些人了解我是教数学课的教师，就跟我说：左教师，你每一次数学考试都能考一百分吗？

我该怎样回应呢？

你说起能，那么就太狂了吧；你说起不可以，正中间提问者的心坎.

因此，我回应：看情况吧.假如总分成150分，我可以考100；假如总分成一百分，那么我考不上.

这儿就用到了分类讨论的观念.

解数学题也一样，当解到某一步时，没法用统一的方式，统一的关系式再次向下，由于被科学研究的难题包括了多种多样状况.

最先要有分类讨论的观念，次之，要寻找分类讨论的规范.

初等数学中，在什么情况要探讨呢？

例如去绝对值要探讨算式的正负极，设平行线要考虑到切线斜率是不是存有，等比数列求饶要考虑到公比是不是为1，分段函数要考虑到带入哪一个函数解析式，二次函数的最值要考虑到变量是不是在定义域以内...

三、数学思想观念

在，，，中，我举了许多 事例来表明.

四、转换与化归思想

续篇就谈这一，敬请关注.

[原創不容易，假如您觉得文中有使用价值，伸伸手指导并分享，便是很好的适用与毫无疑问]

四大观念，相随普通高中

人称赞