斐波那契 神奇的斐波那契数列之“斐波那契” 数列的由来

在小说《达芬奇密码》中，作者丹·布朗描述了被谋杀的馆长雅克·索尼埃在他死前留下了八个数字“13-3-2-21-1-1-8-5”的序列作为关于他命运的线索。密码学家索菲·内夫凭借她良好的数学积累，重新排列了这八个数字，从而理解了它们的含义。

现在让我们来了解一下这个神奇的序列！

13世纪初，列奥纳多的父亲吉列尔莫(威廉)被昵称为波纳奇(意为“好的、自然的”或“简单的”)，所以列奥纳多得到了斐波纳奇(意为波纳奇的儿子菲利斯·波纳奇)，后来发现他和15世纪的一位伟大的艺术家同名，于是为了区别用他的昵称斐波纳奇改名。1202年，在他27岁的时候，他把他所学到的东西写进了《计算之书》(Liberabaci)。这本书通过新的数字系统在会计、重量计算、利息、汇率和其他应用中的应用展示了它的实用价值。这本书极大地影响了欧洲人的思维。这本书在1228年的修订版中记录了许多有趣的问题。斐波那契死于1250年。在随后的几百年里，欧洲数学家没有研究数学的社会环境，斐波那契的不朽之作也暂时被冷落。直到300年后，人们才开始关注他的遗产，开始对一个看似普通，背后隐藏着一个伟大世界的“养兔问题”产生兴趣。

斐波那契在《计算之书》中提出了一个有趣的兔子问题:如果一对成年兔子每个月刚好生一对小兔子(一雌一雄)。年初，只有一对兔子。第一个月结束时，它们长成成年兔子，第二个月结束时，这对成年兔子将生出一对小兔子。这个生长繁殖的过程会一直持续下去。假设出生的兔子都不会死，一年有几对兔子？

繁殖的过程可以用一棵“家谱”来表示:

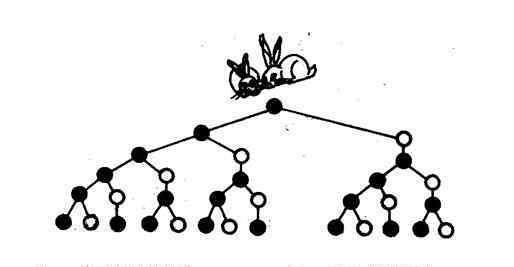
我们来计算一下第五个月末兔子的总数:

第一个月:只有一对兔子；

第二个月:兔子没有长大，还是只有一对兔子；

第三个月:兔子生了一对兔子，此时有2对兔子；

第四个月:老兔子又生了一对小兔子，但是上个月生的兔子还没成熟，此时有3对兔子；

第五个月:此时两对兔子可以繁殖，于是诞生了两对兔子，此时有五对兔子；

基于此计算，不难得出如下结果(如下表所示):

从表中可以看出，一年后(第13个月)有233对兔子。也就是说，仅仅一年时间，一对兔子就可以自由繁殖成233对兔子。多么惊人的繁殖速度！从这个规律来看，难怪兔子会变成灾难！

如果继续这样来来回回，还应该继续做这样麻烦的计算吗？让我们仔细寻找这些数字之间的关系:

即“第n个月的兔子总数=第(n-1)个月的兔子总数+第(n-2)个月的兔子总数”

这部作品是《中国科普——科学原理小知识》的原创。转载时请注明出处。