常数函数 吴国平:数学界的一股清流-常数函数

在数学中，我们把一个值不变的函数叫做常值函数。

如果函数f=8，因为f将任何值映射到8，所以f是一个常数。

更一般地说，对于一个函数f: a → b，如果a中所有x和y都有f=f，那么f就是一个常数函数。

或者我们也讲一下常数函数y =C，如下图所示:

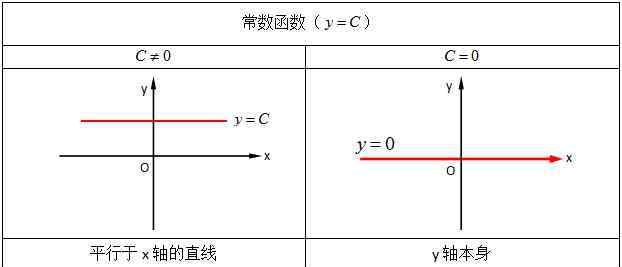
常量函数是最简单的初等函数，即值域只包含一个元素的函数，换句话说就是因变量取固定值的函数。

常数函数的因变量是固定的，也就是说，无论自变量取什么值，其函数值都不会改变。所以其实常量函数也有自变量，比如y=10也可以写成y=0x+10。在没有任何其他限制的情况下，x可以取任何值，也就是所有实数。

值得注意的是，每一个空函数无意义满足上述定义，因为a中没有x和y，这就使得f和f不同。但也有人认为如果包含空函数，常数函数会更容易定义。

复变函数论中的刘维尔定理告诉人们，平面上有界全纯函数只能是常数函数。

常数函数是周期函数，但没有最小正周期。

我们知道，对于函数y=f，如果有一个常数T≠0，使f = f，那么函数y= f称为周期函数，T称为这个函数的周期。

性质1:如果T是函数y=f的任意周期，那么t 的逆也是f的周期。

性质2:如果t是函数f的周期，那么对于任意整数n，nT也是f的周期。

性质3:如果T1和T2都是函数f的周期，T1 T2 ≠ 0，那么T1 T2也是函数f的周期。

对于多项式函数，非零常值函数称为零次多项式；

一个零常数函数可以看作是一个负无穷的多项式。

常数函数可以通过它与复合函数的关系用两种方式来描述。

以下是等效的:

F: a → b是常数函数。对于所有函数g，h: c → a，fog = foh 。f和任何其他函数的组合仍然是常数函数。

上面给出的常数函数的第一个描述是范畴论中更一般的常数态射概念的激发和定义。

根据定义，函数的导函数衡量自变量变化与函数变化的关系。那么我们就可以得到，由于常数函数的值是常数，所以它的导函数为零。

如何证明常数函数的导函数为零，如下:

如果f是在一定区间内定义的实数函数，变量是实数，那么当且仅当f的导函数常数为零时，f是常数。对于预序集之间的函数，常数函数是保序和逆序的；反之，如果f既保序又倒序，如果f的定义域是格，那么f一定是常数函数。

常量函数的其他属性包括:

常数函数没有单调性。

具有相同定义域和伴随定义域的任何常数函数都是幂等的。

任何拓扑空之间的常数都是连续的。

在连通集中，当且仅当f是常数，它是局部常数。