人教版四年级 知识点整理|数学人教版四年级下全册知识点归纳

01

第一单元四项操作

1、加减法的含义和各部分之间的关系

6.租船的问题。

解决租船问题的方法:先假设，后调整。

02

单元2观察物体2

1、正确识别从上、前、左观察到的物体形状。

2.观察物体有诀窍。先看几张脸，再看他们的排列。注意画图形，只画上下。

3.从不同位置观察同一物体时，看到的图形可能相同，也可能不同。

4.当从同一个位置观察不同的物体时，你看到的图形可能相同，也可能不同。

5.只有从不同的位置观察，我们才能更全面地了解一个物体。

03

第三单元操作法

1、加法定律:

①加法交换律:两个数相加，加数位置互换，和不变。

a+b=b+a

2加法组合法则:三个数相加，前两个数可以先相加，然后第三个数相加；或者先把最后两个数相加，再把第一个数相加，和不变。

(a+b) +c=a+(b+c)

③这两个加法定律经常一起使用。

例如:165+93+35 = 93+(165+35)

2.连续减法的性质:一个数连续减去两个数，等于这个数减去那两个数的和。

a-b-c=a-(b+c)

3.乘法定律:

①乘法交换定律:两个数相乘，交换因子位置不变，乘积不变。

a×b=b×a

②乘法组合定律:三个数相乘，可以先乘前两个数再乘第三个数，也可以先乘后两个数再乘第一个数，乘积不变。

(a×b) ×c=a×(b×c)

这两个乘法定律经常一起使用。

例如125×78×8。

③乘法和分配定律:当两个数之和乘以一个数时，两个数可以分别乘以两个数，然后乘积相加。

(a+b) ×c=a×c+b×c

4.连续除法的性质:如果一个数被两个数连续除，则等于两个数的乘积。

a÷b÷c=a÷(b×c)

5.简化计算的扩展:

102×38-38×2

125×25×32

37×96+37×3+37

125×88

3.25+1.98

10.32-1.98

容易出错的情况:

0.6+0.4-0.6+0.4

38×99+99

04

第四单元小数的含义和性质

1.在测量和计算时，往往无法准确得到整数的结果，所以往往用(十进制)表示。

分母为10，100，1000的分数...可以用(十进制)表示；

分母为10的分数可以写成(一位数)小数，

分母为100的分数可以写成(两位数)小数，

分母为1000的分数可以写成(三位数)小数...

因此，十进制数意味着(十)。

两位小数代表(百分比)，

小数点后三位表示的(千分之几)是多少…

例如:

0.5表示(十分之五)，

0.05表示(百分之五)，

0.25表示(百分之二十五)，

0.005表示(千分之五)，

0.025表示千分之二十五)。

2.小数点前的数字称为小数(整数)部分，小数点后的数字称为小数(小数)部分。

3.小数点后第一位是(10)位小数，小数的计数单位是十分之一，可以写成0.1；

小数点后的第二位是百分位数。百分位数的计数单位是1%，可以写成0.01；

小数点后第三位是(千)位小数。千的计数单位是千分之一，可以写成0.001...

比如:20.375，第十位3表示3(十分之一)；百分位数中的7表示7(百分之一)；第千位的5表示5(千分之一)。

4.每两个相邻的小数计数单位之间的进给率为10，(千分之十为百分之一，百分之十为十分之一，十分之十为整数1，或者10 ^ 0.001为一个0.01，10 ^ 0.01为一个0.1，10 ^ 0 ^ 0.1为整数1...

5.读小数时，整数部分要按照整数的读法来读，小数点要读成“点”，每个数字在小数部分要依次读出。

例如，31.031发音为31.031

6.写小数时，整数部分要用整数的方式写，小数点要写在每个数字的右下角，小数部分要在每个数字上依次写数字。

如:120.0098

写作:120.0098

7.小数末尾加“0”或去掉“0”，小数大小不变。这就是所谓的小数的性质。

例如:

0.2= 0.20 = 0.200 =0.2000 =……

1.05=1.050 =0.0500 =0.0500=……

1.080=1.08

10.0800=10.08

100.080000= 100.08

8.十进制大小的比较:

先比较整数部分，整数部分大，小数大；如果整数部分相同，比较小数部分，如果小数部分相同，比较百分位数，如果百分位数相同，比较第千位...

9.小数点的移动:

12.为了读写方便，往往需要将不是一万或一亿的整数改写成以“一万”或“一亿”为单位的数字。重写时，只需在10000或10000万位数字的右边加一个小数点，数字后加“10000”或“10000万”字。

05

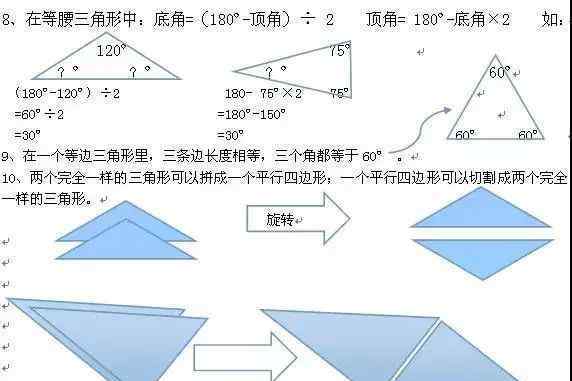
第五单元三角形

1.由三条线段(每两条相邻线段的端点相连)围成的图形称为三角形。例如:

2.从三角形的一个顶点到它的对边做一条垂直线，顶点和垂足之间的线段称为三角形的高度。这个相对的边叫做三角形的底部。例如:

6.三角形根据边可以分为等腰三角形、等边三角形和等边三角形。例如:

7.三角形的三个内角之和是180度。

06

第六单元小数的加法和减法

1、写十进制加减法:

⑷整数乘法的运算法则也适用于十进制乘法

例如3.65×42.6+3.65×57.4

5]在十进制运算中，可以使用(加括号)或(去掉括号)使计算变得简单:

→是去掉括号还是增加括号

(1)括号前面是一个加号，去掉括号的常数；

例如6.59-4.86+2.86

②括号前有减号，去掉括号改变整数(加号变成减号，减号变成加号)。

例如6.47-(1.5-0.53)

[6]在没有括号的同级别操作中，交换数据的位置必须取其前面的符号。

例如4.95-2.67+1.05

07

第七单元图形的运动2

1.沿着某条线把一个图形对折。如果线两边的部分可以完全重合，我们就说图形是轴对称的，这条线叫做图形的对称轴。

2.轴对称性:对应点到对称轴的距离相等。

3.对称轴是直线，所以画对称轴时要画在图外，要用虚线。

4.正方形对角线所在的直线就是它的对称轴。轴对称图形可以有一个或几个对称轴。

5.画对称轴时，先找到与对称轴方向相反且相同的对应点，最后连线。

6.长方形、正方形、等腰梯形、等腰三角形、等边三角形、线段、菱形都是轴对称图形。

矩形有两个对称轴，

正方形有四个对称轴，

等腰梯形具有对称轴，

等腰三角形有对称轴，

等边三角形有三个对称轴，

线段具有对称轴，

钻石有两个对称轴，

一个圆有无数对称轴，

有一个半圆，

有无数个戒指，

有一个半圆。

7.平行四边形不是轴对称图形，没有对称轴。(矩形和正方形除外)

8.梯形不一定是轴对称图形。只有等腰梯形是轴对称的。

9.古今中外很多著名建筑都是对称的。例如:中国的赵州桥，印度的泰姬陵，英国的塔桥，法国的埃菲尔铁塔。

10、翻译要找图形点，翻译点在一起，注意点数要数十字。

11、平移不改变图形的大小和形状，只改变图形的位置。

12.使用平移，可以计算不规则图形的面积。

08

第8单元平均值和条形图

平均值:

1.平均方法:

(1)数据少:多动少补。

(2)常用方法:先算后除:总数÷份数=平均数

2.平均值可以清楚地表明一组数据的整体水平。

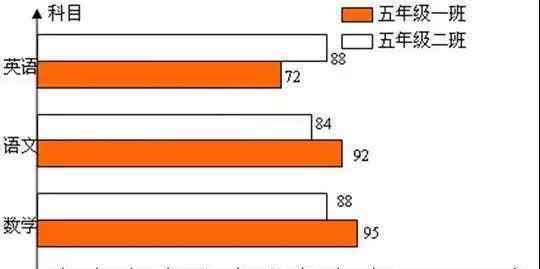
条形图:

将两个单独的条形图合并后，得到一个复合条形图。

多个条形图应该有图例。

复合条形图有两种:水平和垂直。

复合条形图是用两个单位长度来表示一个的数量，并根据数量画出不同长度的直杆。

如何绘制水平复合条形图

1.准备好绘图工具，如尺子、铅笔和橡皮。

2.注意书写单位。图中有坐标和横坐标，横坐标上有日期名称和“0”。

3.如果位置有限，比如0到10，到20，如果写200，位置绝对有限，可以在0上画一条波浪线再写100(当然其他数字也可以，不过最标准的是画一条闪电线)。

4.比如上图，两者颜色应该不一样。如果没有彩笔，第一支可以画对角线，第二支可以画牢固。

5.在每张图片的底部写一个标题。

复合条形图:

【特征】直杆的长度用来表示数量。【优点】数字看的很清楚，方便比较两组数据。

之后，按照一定的顺序排列这些直杆。从复合条形图中很容易看出两者的数量。

09

第九单元数学广角——同笼的鸡和兔

1.鸡和兔子住在同一个笼子里是一个假设问题，与最终结果相反。

2.解决“鸡兔同笼”问题的方法

假设方法:

(1)如果它们都是兔子

2如果都是鸡，

③古人“抬脚法”:

解决方案想法:

如果每只鸡和兔子都把脚抬起一半，那么每只鸡就变成了“一条腿的鸡”，每只兔子就变成了“两条腿的兔子”。这样，鸡和兔子的脚总数减少了一半。这种思维方式叫还原。

3.公式:

鸡兔总足数÷2-鸡兔总足数=兔数；

鸡兔总数-兔数=鸡数。

-结束-