derivation 无工质微波推进理论（中英对照）

航天器微波推进理论

无工质微波推进理论

原作者:罗杰·肖耶

罗杰·苏亚，工程技术学院特许工程师

翻译:光年

本文最后介绍了一种新的Emdrive结构，详见第页。

来源:www.emdrive.com

卫星推进研究有限公司2006

本文件的版权归卫星推进研究有限公司所有

本文件英文原文内容的版权所有者为卫星推进研究有限公司..

摘要摘要

介绍了一种航天器电推进的新原理，利用微波技术实现直流功率直接转换为推力，无需推进剂。

介绍了一种新的电磁空推进理论，该理论利用微波技术实现电力推力的直接转换，无需工质。

给出了工作原理的简化说明，接着从第一原理推导出了这种装置的推力方程。能量守恒定律的含义在装置的静态和动态操作中都进行了检验。

首先讨论了简化原理，然后从第一个原理出发推导了无工质微波推进的推力方程。它遵守能量守恒定律，可以从静态和动态两方面验证无工质微波推进设备。

1.基本原则

本文描述的技术在发动机中使用微波频率的辐射压力，该发动机提供从微波能量到推力的直接转换，而不需要推进剂。

本文描述的技术使用辐射压力。在微波波段，发动机的推力直接由微波能转换而来，不需要推进剂。

微波发动机的概念如图1所示。微波能量从磁控管通过调谐馈电馈送到封闭的锥形波导管，其总电长度在磁控管的工作频率下产生谐振。

微波引擎的概念如图1所示。磁控管产生的微波能量经过调节后进入一个封闭的锥形波导腔，其形状和电长度使工作微波发生共振。

如果用电磁波的群速度vg代替v，则等式1说明，如果vg1大于vg2，则Fg1应该大于Fg2。

如果用电磁波的群速度vg代替v，那么方程1表明，如果vg1大于vg2，Fg1应该大于Fg2。

然而，由于波导两端的速度是光速的重要部分，力差方程的推导需要速度差，因此必须考虑狭义相对论。

但由于锥形波导两端的速度接近光速，推力差分方程的推导要考虑速度的差异和狭义相对论的影响。

相对论意味着电磁波和波导组件形成一个开放的系统。因此，力差导致作用在波导组件上的推力。

相对论是指电磁波和波导器件形成一个密闭系统。因此，由压力差引起推力作用在波导器件上。

2.推力方程的推导

考虑一束光子垂直入射到平板上。设光束的横截面积为A，假设它由每单位体积n个光子组成。每个光子都有能量hf，以速度c传播，其中h是普朗克常数，f是频率。入射光束的功率是。

考虑微波束的垂直入射面。假设这个微波每单位体积有n个微波光子，让它通过一个横截面积A。每个微波光子的能量hf和速度c，h是普朗克常数，f是频率。然后是入射微波束的功率。

每个光子的动量为hf/c，因此光束在平板上的动量变化率为2nhfA。将动量的变化等同于作用在板上的力F0，我们发现

每个光子的动量为hf/c，束板动量的变化为2nhfa。这个动量变化作用在平面上的力是F0，得到方程

这是麦克斯韦得到的辐射压力的经典结果。这里给出的推导是基于库伦。如果梁的速度为v，那么板的动量变化率为2nhfA，因此在这种情况下，板上的力Fg由下式给出:

这是通过麦克斯韦辐射压力的经典结果。这里给出的推导是基于卡伦。如果作用在平面上的微波束的速度v和动量变化为2nhfa，在此条件下，得到平面力Fg方程:

我们现在假设光束进入一个充满真空的波导管。波导从波长为λ0的自由空间传播逐渐变细，直至给出波长为λg、传播速度为νg的波导尺寸。这是群速度，由下式给出:

假设微波束在真空中进入锥形波导器件，在自由空中进入锥形波导器件，微波束波长λ0，锥形波导中波长λg，传播速度ν g，微波束群速度方程；

然后，从和可知，封闭波导管末端的板上的力为:

然后，从方程和，推导出锥形波导器件端面上的力方程:

第二个效应是，由于光束速度不直接取决于波导的任何速度，光束和波导形成一个开放系统。因此，端板处的反应并不局限于波导和光束的封闭系统，而是波导和光束之间的反应，在开放系统中，每个反应都在各自的参考系内进行。

第二个作用是微波束的运动不直接依赖于锥形波导器件的运动，微波束和锥形波导器件形成一个开放系统。因此，端面上的相互作用不能牵强地认为是锥形波导器件和微波束的闭合系统运动，而是锥形波导器件和微波束之间的相互作用，它们有自己的参考系，构成一个开放的非闭合系统。

从和我们发现:从公式和获得:

Where λd is the wavelength in the unbounded dielectric medium and Vg3 is the guide wavelength at the end plate of the dielectric section. It then follows that the thrust takes the form：其中λd是无界介质中的波长，Vg3是介质部分端板的波导波长。接下来，推力的形式是:

λd是电介质中的微波波长，Vg3是微波在端板和电介质部分中的移动速度。得到推力方程:

Where其中：哪里哪里:

我们假设复合波导在微波束的频率下谐振，并且导电和介电损耗使得存在Q个返回路径。那么总推力最终由下式给出:

假设复合锥形波导器件的谐振与微波束频率匹配，考虑导体和介质损耗，存在Q个返回路径。得到总推力方程:

3.发动机的动态运行。无工质微波推进的动力学分析

我们现在研究能量守恒原理的含义，当推力第一次在静态试验台架上测量时，然后当发动机用于加速航天器时。

本文讨论了受力状态下能量守恒定律的应用，首先是静态试验台推力的测量和分析，然后讨论了无工质微波推力器加速航天器的问题。

当微波发动机安装在静态试验台架上时，所有输入功率P0都转换成电损耗。在这种情况下，发动机的Q可以被称为Qu，即空载Q

将无工质微波推力器安装在静态试验装置中，其输入功率P0转化为电损耗。在这种情况下，没有工作介质的微波推力器的q变成了Qu，没有负载q值。

现在在他们中间

其中Pc是谐振波导内的循环功率，Pe是电损耗。从我们发现:

锥形波导器件中的光子晶体谐振循环功率，电子损耗。根据等式:

Where Df is the design factor：其中Df是设计因素:

其中Df是设计因素:

然后又得到了

因此，如果循环功率保持不变，例如在超导谐振波导中，那么T将保持不变。这在非航天器应用中很重要，在非航天器应用中，曲值很高可以用来提供恒定推力以对抗重力。

循环功率保持不变，例如在超导谐振锥形波导器件中输入功率时，推力t会保持不变。在非航天领域的一个重要应用是，当品质因数Q很高时，可以用来提供恒定推力抵抗重力。

如果发动机安装在总质量为M的航天器上，并被允许在时间t内从初始速度vi加速到最终速度vf，那么通过使动能相等，我们得到:

无工质螺旋桨安装在总质量为m的航天器上，从初始速度加速vi最终速度vf所需的时间t，动能方程为:

这里Pk是传递给飞船的输出功率。由此我们获得:

Pk是微波推进器传递给航天器的有效功率。再来一次

v是时间t上的平均速度，a是航天器的加速度。现在M.a是由于宇宙飞船加速产生的力，它是相反的。

时间t中v的总速度矢量，航天器的加速度。目前M.a是作用在航天器上的力的绝对值，与微波推进器产生的推力相反。

然后又得到了方程

其中Ql是发动机输出功率Pk时的负载Q。

电功率损耗被假定为I2R损耗，

当微波推力器输出功率为Pk时，Ql为微波推力器的有效输出能量。电损耗功率假定为I2R，适用于所有质量因素:

其中Pe0是Q=1时的损失。从静态情况来看，我们有

Pe0是Q=1时稳态分析得到的方程

So that For an accelerating spacecraft,所以对于加速的宇宙飞船来说，

所以，对于加速的宇宙飞船来说，

将和代入最后一个方程，得到。

替换等式和等式以获得方程组:

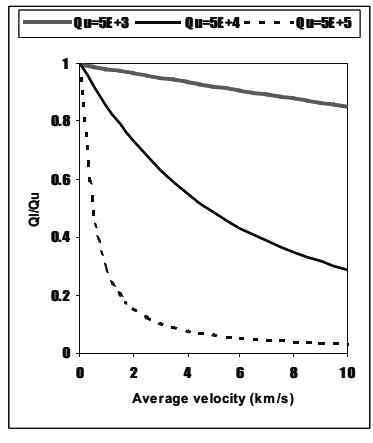
图3.1显示了对于高达10km/sec的v值和等于5x103、5x104和5x105的Qu值的的解。Df值取为0.945，由图3.1中使用的相同群速度得出

图3.1所示的方程组的解v的值为0 ~ 10km/s，qu的值等于5 x103 5 x104 5 x105。Df值为0.945，同一组速度的关系图如图3.1所示

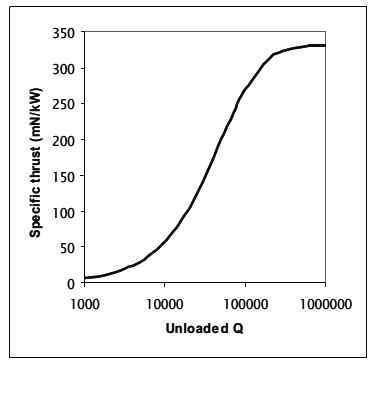
对于等于0.945的Df和3 km/s的平均速度，比推力由和获得，并在图3.2中给出。这说明在这个速度下，比推力增加到最大值333毫牛顿/千瓦。

Df=0.945，平均速度3公里/秒和推力之间的关系在图3.2中用公式和公式表示。在这个速度下，图3.2显示最大推力为333毫牛顿/千瓦。

4.结论

一种推进技术的理论已经发展出来，这种技术第一次允许从微波频率的电能直接转换成推力。从第一性原理发展出一个表达式，使这种技术的推力可以计算出来。这个表达式已经被在实验推进器和演示发动机上进行的两个试验程序的结果所验证。

随着推进技术的理论发展，首次允许通过微波直接将电能转化为推力。本文从第一个原理，推导出推力的计算。这个表达式的结果在这两个试验项目中得到了验证。

对能量守恒原理的考虑导致了用于以轨道速度加速航天器的发动机的负载Q的方程式的推导，这允许预测推力。航天器系统在消除对推进剂的需求方面的优势，以及预测的比推力，为总体任务性能提供了重大改进。

基于能量守恒定律，推导出微波推力器航天器在轨道速度下所需能量方程的Q值，从而给出推力的预测。这种航天器的优点是不需要推进剂，推导出能量-推力比，对整体性能的提高是一个很大的改进。

感谢

作者感谢SPR有限公司的同事、邓迪阿伯塔伊大学的R . B . Paris博士、阿斯特里姆英国有限公司的J W .斯皮勒和利物浦大学的J .卢卡斯教授给予的帮助。理论工作和实验方案是在贸易和工业部的支持下，根据科学、技术和创新奖励计划，然后根据研究和发展赠款进行的。

作者非常感谢SPR同事的帮助，也感谢巴黎阿伯塔伊大学的RB博士。阿斯特里姆英国有限公司斯皮勒的阿斯特里姆和利物浦大学教授卢卡斯。在贸易和工业部门的支持下，在他们的智能激励计划下开展了理论和实验工作计划，并为研究和开发提供了资金。