奥数题六年级 小升初六年级奥数题及答案 20道题（中等难度）

今天给你带了20个六年级的奥数练习题~

练习一下，看看你能做对多少。答案在文末分析

【标题-006】灌水问题:(中等难度)

公园游泳池需要每周换一次。进水管有A、B、C三根，第一周小李按A、B、C、A、B、C的顺序打开小的那根，刚打开一根进水管一小时就灌满了水池空。第二周按B、C、A、B、C、A，第三周按C、B、A、C、B、A的顺序轮流打开一个小时，比第一周多15分钟。第四周，他的三根管子同时打开，用了2小时20分钟灌满了一池水。第五周，他只打开了第一根管子，所以用了_ _ _ _ _ _ _ _ _个小时灌满了一池水。

【题目-007】专注力问题:(中等难度)

瓶子里装1000克15%酒精溶液，现在分别倒入100克和400克A、B酒精溶液，瓶内浓度变成14%。已知A醇溶液的浓度是B醇溶液的两倍，那么A醇溶液的浓度是多少呢？

水和牛奶:(中等难度)

一个卖牛奶的告诉两个小学生，一个钢桶里有水，一个钢桶里有牛奶。因为乳霜含量太高，喝之前一定要稀释。现在我把A桶的液体倒入B桶使其体积翻倍，然后我把B桶的液体倒入A桶使其体积翻倍。最后，我把A桶里的液体再倒进B桶。把B桶的液体体积翻了一倍，这时候我发现两桶装的液体量是一样的，而B桶的水比牛奶多1升。现在想问问大家，开始的时候有多少水多少奶，最后每个桶有多少水多少奶？

[Title -009]巧妙计算:(难度适中)

计算:

【标题-010】阵型:(难度适中)

做少年广播体操的时候，某年级的学生站成一个实心的正方形(正方形队列)的时候，还是多了10个人。如果他们站在一个实心的正方形中，每边多一个人，仍然有15个人失踪。问:当时有多少人？

[标题-011]计算:(中等难度)

如果奇数位上的数字总和与偶数位上的数字总和之差是11的倍数，如1001，则自然数是11的倍数。因为1+0=0+1，是11的倍数。再比如1234，因为4+2-(3+1) = 2不是11的倍数，所以1234不是11的倍数。问:6个数字，0，1，2，3，4，5，用来组成6位数字，没有重复的数字，有多少是11的倍数？

【标题-012】评分:(难度适中)

某学校部分学生成绩总和是8250分。一、二、三年级学生成绩分别为88、85、80分，最低30分，同一分不超过3人。每个学生的分数都是自然数。问:至少有几个学生的分数不低于60分。

[标题-013]四位数:(中等难度)

一个四位数有以下特点:①这个数加1后是15的倍数；2这个数字减3是38的倍数；(3)把这个数的每个数字上的数反相得到的数和原数之和可以被10整除，就可以得到四位数。

[标题-014]行程:(中等难度)

王强骑自行车去上班，并以统一的速度旅行。他观察过往的公交车，发现每隔12分钟就有一辆车从后面经过，每隔4分钟就有一辆车迎面而来。如果所有的车都以相同的匀速行驶，发车间隔相同，那么调度员每隔几分钟就派一辆车？

[标题-015]跑步:(中等难度)

狗跑5步，马跑3步，马跑4步，离狗跑7步。现在狗已经跑了30米，马开始追它。问:狗能跑多远，马能追上它？

【标题-016】排队:(难度适中)

一个圆有五对，这样每对的对可以移动相邻的行()

[标题-017]分数方程:(中等难度)

几个相同的盒子排成一排。小聪把42个一模一样的球放在这些盒子里，然后出去了。小明从每个盒子里拿出一个球，放在球数最少的盒子里。我又重新排列了盒子。小聪回来了，仔细看了看。没人碰球和盒子。问:有多少个盒子？

自然数之和:(中等难度)

在整数中，有两种方法可以用两个以上连续自然数的和来表示一个整数。比如9: 9 = 4+5，9=2+3+4，9有两种方式用两个以上连续自然数的和来表示。

[标题-019]准确值:(中等难度)

【标题-020】巧找整数部分标题:(难度适中)

(第六届十进制报期末考试)A 8.8 8.98 8.998 8.9998 8.99998，A的整数部分是_ _ _ _ _ _ _。

这个公式和我们常见的分数项的区别在于，每个项的分子依次变成等差数列，而不常见的分子是相同的或者分子是分母的差或和。所以分子要适当变形，转换成熟悉的形式。

方法1:

观察表明5=2+3，7=3+4，...也就是说，每个项的分子等于分母中前两个乘数的总和，因此

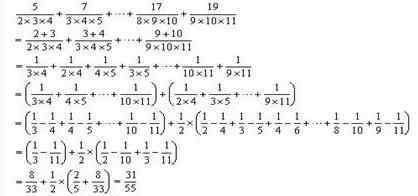
[问题-010解决方案]形成

扩展正方形矩阵时，要加10+15个人，这25个人要站在扩展的正方形矩阵的相邻两边，形成一个由人组成的直角拐角。加人后，展开的正方形矩阵两边各有(10+15+1)÷2=13人。所以扩展后的方阵有13×13=169人，去掉15人，就是原来的那个。

169-15=154人

[问题-011解决方案]计算答案:

用1.2.3.4.5组成六位数字，无重复数字，

，可以被11整除，且设a1+a3+a5≥a2+a4+a6，则对于k≥0的整数，有:

a1+a3+a5-a2-a4-a6=11k (*)

即:

a1+a2+a3+a4+a5+a6 = 11k+2(a2+a4+a6)

15 = 0+1+2+3+4+5 = 11k+2(a2+a4+a6)(*)

可见k只能是奇数

从公式(*)可以看出，0 ≤ k

但是0，1，2，3，4，5中任意三个数之和不等于2，所以k≠1。所以，(*)不成立。

在a2+a4+a6 > a1+a3+a5的情况下，同样可以证明(a2+a4+a6)-(a1+a3+a5)不是11的倍数。

根据以上分析可知，0、1、2、3、4、5不能用来构成不重复数就能被11整除的六位数。

【问题-012答案】评分:(难度适中)

除了88、85、80分的人，其他人的分数都在30到79分之间，其他人的总分都是8250-(88+85+80) = 7997。

为了尽量减少不低于60分的人数，需要尽量增加低于60分的人数，即得分30 ~ 59分的人数尽可能多，最多3 × (30+31+...+59) =这些分数上的4005分(总分)。所以60 ~ 79分的人最多能拿到总共7997-4005 =的分数。

如果有60个人拿60分到79分，占3 × (60+61+...+79) = 4170，比最高分7997-4005= 3992多了178分，所以要从不低于60分的人群中剔除尽可能多的人。但很明显，最多只能去掉两个不低于60分的人(加一个不低于60分的)。

[问题-013答案]四位数:(中等难度)四位数答案:

这说明m=27，37，47；32, 42, 52.(因为38m的尾数是6)

而且因为38m+3 = 15k-1 (m和k为正整数)，38m+4=15k。

由于38m的位数是6，5 | (38m+4)，

所以38m+4=15k相当于3 | (38m+4)，也就是3除以m等于1，就可以知道m=37，m=52。

要求的四位数是1409，1979。

[问题-014答案]行程答案:

车与车之间的距离相等，列出的方程为:(车速-自行车速度)×12=(车速+自行车速度)×4

结果表明，汽车速度=两倍自行车速度，汽车发车间隔时间=车距÷汽车速度=(两倍自行车速度-自行车速度)× 12 ÷两倍自行车速度=6(分钟)。

【问题-015回答】跑步:(难度适中)

根据“马跑4步和狗跑7步的距离”，可以假设马的每一步长为7x米，狗的每一步长为4x米。

根据“狗跑5步，马跑3步”可知，马同时跑3*7x米= =21x米时，狗跑5 * 4x = 20x米。

可以得出结论，马与狗的速度比为21x: 20x = 21: 20

根据“狗现在已经跑了30米”，我们可以知道狗和马的距离是30米，两者之差是21-20 = 1。现在21匹马的距离是多少，也就是30 ÷ (21-20) × 21 = 630米

【问题-016答案】排队:(中等难度)

根据乘法原理，它分为两步:

第一步，把五对看成五个整体，用5× 4× 3× 2× 1 = 120种不同的排列方式进行排列。但是因为是首尾相接围成一个圈，所以会有5次重复，所以实际的排列方式只有120 ÷ 5 = 24。

第二步，每对可以互相变换位置，也就是说每对有两种排列方式，总共2 × 2 × 2 × 2 = 32种

综合两步，有24 × 32 = 768

【问题-017解答】分数方程:(中等难度)

假设球数最少的盒子里装的是A球，现在加的是B球。因为小聪没发现有人摸球和盒子，说明现在有一个装A球的盒子，原来装的是(a+1)个球。

同样，现在还有一个装(a+1)球的盒子，原来装的是(a+2)球。

以此类推，还有一个盒子，里面装着(a+3)个球，(a+4)个球，等等。所以这些盒子里的球数是一些连续的整数。

现在变成:把42除以几个连续整数的和，有多少种除法，每种除法有多少个加数？

因为42=6×7，可以认为是7个六的和，(7+5)+(8+4)+(9+3)是6个六，这样42=3+4+5+6+7+8+9，一共7个加数。

而且因为42=14×3，42: 13+14+15可以作为三个加数相加。

因为42=21×2，42=9+10+11+12可以相加，有4个加数。

所以原问题有三种解决方案:7盒，4盒或者3盒。

【问题-018解答】自然数之和:(中等难度)

(1)请写出只有三个这样表示的最小自然数。

(2)请写出只有6个这样表示的最小自然数。

关于一个整数，它的“奇数除数减1”是指物种数以连续整数之和的形式表示。

根据(1)，我们知道有三种表示方法，所以奇数除数为3+1=4，4的质因数为4=2×2，最小值为15(1，3，5，15)；

有连续的2、3、5个数相加；7+8;4+5+6;1+2+3+4+5;

根据(2)，我们知道有6种表示方法，所以奇数除数为6+1=7，最小值为729(1，3，9，27，81，243，729)，并有2，3，6，9，10，27的连续数相加:

364+365;242+243+244;119+120+…+124;77+78+79+…+85;36+37+…+45;14+15+…+40

【问题-019解答】准确值:(中等难度)

【问题-020解答】巧妙找到问题的整数部分:(中等难度)