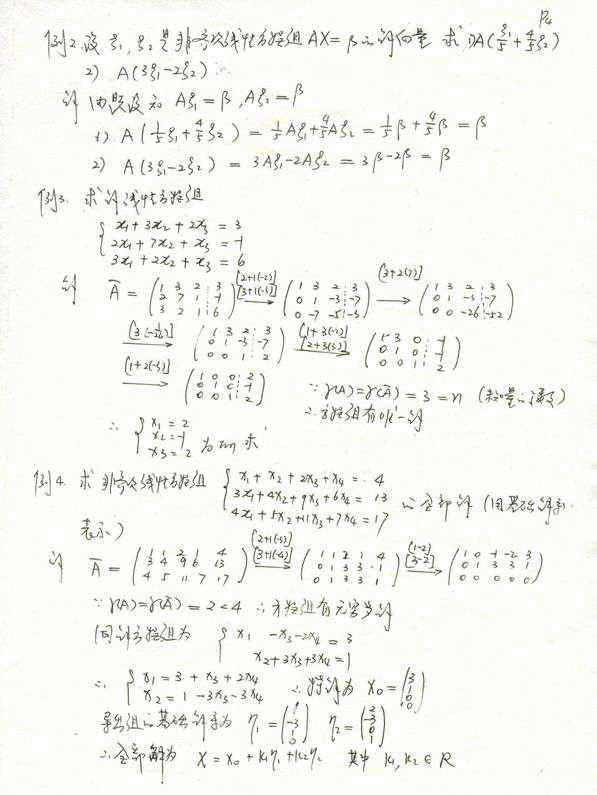题目:
已知直线的极坐标方程为ρsin(θ+π/4)=(2^1/2)/2,求点A(2,7π/4)到这条直线的距离能够给出详细解答过程者,追加30分
解答:
1.把直线的极坐标方程化为直角坐标系方程:ρsin(θ+π/4)= √2/2ρ(sinθcosπ/4+cosθsinπ/4)=√2/2ρ(√2/2 sinθ+√2/2 cosθ)=√2/2ρ sinθ + ρ cosθ=1即:y+x=12.把点A(2,7π/4)化为直角坐标系下的点:x=ρ cosθ=2*cos7π/4=√2y=ρ sinθ=2*sin7π/4=-√23.题目化简为:求点A(√2,-√2)到直线y+x=1的距离;根据公式d=|x+y-1|/√(1+k^2)=|√2-√2-1|/√(1+1)=√2/2."√"代表根号.
1.《直线的极坐标方程 已知直线的极坐标方程为ρsin(θ+π/4)=(2^1/2)/2,求点A到这条直线的距离》援引自互联网,旨在传递更多网络信息知识,仅代表作者本人观点,与本网站无关,侵删请联系页脚下方联系方式。
2.《直线的极坐标方程 已知直线的极坐标方程为ρsin(θ+π/4)=(2^1/2)/2,求点A到这条直线的距离》仅供读者参考,本网站未对该内容进行证实,对其原创性、真实性、完整性、及时性不作任何保证。
3.文章转载时请保留本站内容来源地址,https://www.lu-xu.com/jiaoyu/428198.html