洛必达 一篇文章，讲清楚洛必达

洛必达法则

这里没有严格的极限定义，因为高中数学课本上没有极限的定义。

先说一个简单的概念:不定式。

假设我们有两个函数

和

，如果什么时候

什么时候，有

，这叫分数

为

类型不定式；

同样，如果

什么时候，有

和

(这里的无穷大可以是正的也可以是负的)叫做分数

为

键入不定式。

以上是使用洛必达定律的前提条件，只有满足条件才能“失去”。

洛必达定律的内容如下，分为

键入不定式和

键入不定式。

定理1(

键入不定式)if when

当，

为

键入不定式，

和

存在，并且

不是不定式

；

定理2(

键入不定式)if when

当，

为

键入不定式，

和

存在，并且

不是不定式

。

要解释这个定理，只需要导数的定义。

(需要注意的是，我这里用的词是“解释”，而不是“证明”。希望你不要有“证据可以用”的想法。)

先考虑定理1，根据导数的定义，

。

然后

，其中

，并且根据

换人就能拿到

这是理想的结果。

再次考虑定理2，当

什么时候，如果

，那么

，记得吗

,

，那么

是

应用定理1的不定式类型:

另一方面，有

，从这个解决方案

，也就是，

。

在这一点上，可以(松散地)解释上述结论是有效的。

二、洛必达定律的小应用

举几个简单的例子说明高中如何使用洛必达定律。

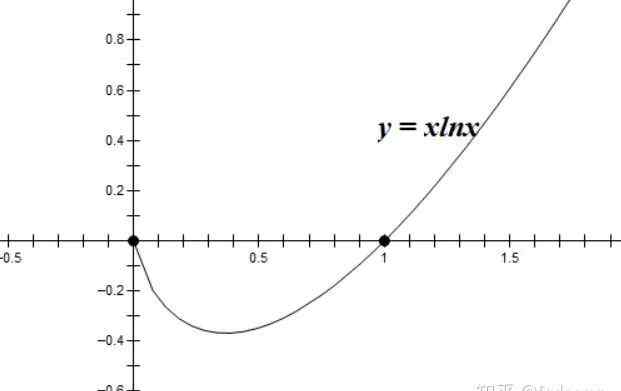
示例1绘制函数

的形象。

解是导出的

，因此

在

减少，在

增量。

经过计算。

,

，那就分析一下什么时候

当...的时候

的价值。

，此时发现

和

都趋向于无穷大。使用洛必达定律:

，因此

。

示例2当

时间不平等

不断建立，现实的数字

的值范围。

求解分离参数的

，制作

，其中

。

，制作

,

，因此

在

单调递增，

，因此

,

在

单调递增。

要求

恒是成立的，所以

，但是什么时候

当，

，这是

键入不定式。根据洛比达定律，有:

，因此

，实数

的值范围是

。

示例3当

时间不平等

不断建立，现实的数字

的值范围。

回答

，再次

，因此

。

当...的时候

当，

，实数

的值范围是

。

即使是洛必达也可以“lo”很多次，只要是不定式，就可以“lo”直到得出结果。

例4求极限

。

回答什么时候

当，

，使用洛必达定律:

，此时仍得到不定式。

当...的时候

当，

，再次使用洛比达定律:

，因此

。

第三，洛必达能用吗？如何规避洛必达定律？

其实我反复强调过，高中数学没有极限的定义，以上过程也不严谨。

各省标准不同，有的地方可能会给分，有的地方可能会酌情扣分，有的地方甚至可能不会给一分。

洛必达定律原本是高等数学中一个非常有用的结论，但“洛必达”最终成了一些高中生强行使用的词汇。他们遇到题目的时候，以为可以杀人，但是完全没有考虑到严谨性。

另外，很多高中生随机“lo”不带不定式，最后得到一个完全错误的答案。结果这些人开始到处问“为什么这个问题不能是洛必达？”“洛必达错了吗？”。

其实在做题的过程中，完全可以绕过洛必达定律，达到同样的效果。

一般来说，遇到恒成立问题时，不等式是可以分离的，形式如下

的形式，在哪里

的临界值是

，和

。那么很多人会用洛必达定律来找答案

在

的极限

。但是有必要这样做吗？

如果

，那么

，制作

，原来的不等式相当于

。我们试图分析构造的函数。

当...的时候

当，

一般来说，让我们只是让

在

在单调减少之前，在

之后会单调增加。

也就是，

是

最低限度，使

，可以解决

，这和我们用洛必达定律得到的结果是一样的。

但是如果

我该怎么办？你可以再求一次导数，然后做出来

，从这个解决方案

，就像多次应用洛必达定律一样。

从这个角度来看，“洛必达定律”完全没有出现在题目中的必要。使用洛必达实际上相当于直接求构造函数的多个导数。

解题时可以用洛必达定律猜答案，但写过程时要用分类讨论的方法把过程写清楚。

对了，我也提醒高中生不要盲目的寻求一些“二杀”的方法，反而会弄巧成拙。

-文章来源-

*声明:图文源网。如有侵权，请联系删除。转载请注明出处。更多信息请关注微信微信官方账号高考(高考010)。