FLUENT中的“湍流模型”是什么东西？

众所周知流体的流动状态有层流和湍流的分别。工程中大部分的流动都是湍流，所以用CFD软件模拟工程中的流动的时候，往往要运用“湍流模型”，例如k-ε模型、SA模型等等。但是，这些模型是怎样模拟湍流流动的呢？

我们来看一个例子。我们用k-ε模型计算二维射流流动。当流体从一个狭缝向静止流体中喷射的时候，如果狭缝的长度比宽度大得多，那么就可以近似地看做是二维射流。二维射流理论上的流动图像如图1所示。由于粘性作用，射流与周围流体之间进行动量交换，并把周围流体不断“卷吸”到射流中去，使得沿着流动方向射流的宽度不断向外扩展。

图1 二维射流。

假设缝隙的宽度h=1m，喷射速度U=1m/s，流体的密度ρ=1kg/m3，粘性系数μ=10-5Pa•s，则流动雷诺数Re=ρUh/μ=105。用FLUENT算出的速度分布如图2所示；可以看出沿着流动方向射流的宽度不断向外扩展。从图3所示的不同截面处的速度分布曲线也可以看出这一点。

图2 速度分布

图3 不同截面处的速度分布曲线

从定性上看，粘性导致的动量交换使得沿着流动方向射流的宽度不断向外扩展，这是容易理解的。从定量上看又如何呢？我们选取流场中的几个位置，计算一下动量方程中各项的数值。所选取的三个点如图4所示。

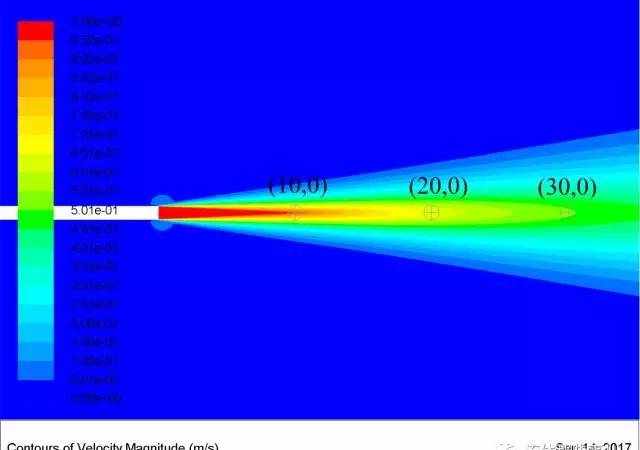
图4 点的位置

我们知道，流体运动的动量方程是Navier-Stokes方程组，对于本问题中的二维不可压缩流动，Navier-Stokes方程组的形式为

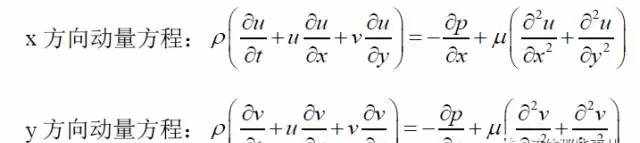
式中u是速度的x方向分量，v是速度的y方向分量，p是压强。由于本问题考虑的是定常流动，所以对时间的偏导数的项等于零，方程简化为

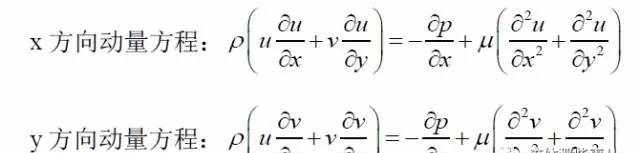
由于射流是往x方向喷射的，所以我们只计算x方向的动量方程，结果如表1所示。显然，动量方程的左边不等于右边，而且数量级相差甚远。

表1 x方向动量方程左边和右边的数值

这是什么回事呢？原来，FLUENT在计算湍流流动的时候，并不是直接求解Navier-Stokes方程组。

要理解这个问题，必须先了解湍流运动的特点。从下面的湍流射流的视频可以看出，湍流中存在不规则的非定常的旋涡运动。研究表明，湍流中的这些旋涡运动的尺度范围是非常宽广的，最大的旋涡与最小的旋涡的尺度之比正比于流动雷诺数的3/4次方。最大的旋涡从平均流中吸收动能，然后将动能传递给小一级的旋涡，小一级的旋涡又将动能传递给更小一级的旋涡，就这样一级一级地往下传递，直到动能传递至最小尺度的涡时，才被粘性耗散转变为热能。这就是湍流中所谓的“能量传递的级串原理”。

由于湍流中旋涡运动的尺度范围非常宽广，直接运用Navier-Stokes方程组对它进行模拟是非常困难的，特别是高雷诺数湍流。举一个直观的例子，一辆以105km/h行驶的轿车，其前挡风玻璃表面的湍流边界层中的最小涡的尺度约为0.004毫米[3]。试想，如果要对这辆汽车的绕流流动进行直接模拟，那么计算域应该包含整辆汽车，而网格尺寸却又要小于最小涡的尺度，其计算量简直是天文数字，目前世界上运算速度最快的超级计算机也望尘莫及。

因此，目前在工程中运用CFD软件来模拟湍流时，普遍采用的是雷诺平均的方法，也就是将湍流中的非定常的旋涡运动（湍流脉动）取平均运算，得到湍流的平均运动。从下面的视频中可以获得对平均运算的直观理解。

FLUENT在计算湍流流动的时候，实际上求解的是湍流的平均运动。我们在观看计算结果的云图时，图中所显示的速度、压力其实都是平均运动的速度和压力。

但是这带来一个问题。我们知道，在层流流动中，根据牛顿内摩擦定律，粘性切应力等于速度梯度乘以粘性系数；这种粘性切应力产生的原因是存在分子不规则运动的动量交换以及分子间的吸引力。但是，在湍流流动中，用平均运动的速度梯度乘以粘性系数来计算切应力是不恰当的。这是因为，在湍流流动中，非定常旋涡运动使得相邻的流体层之间有很强的动量交换效应，这种动量交换效应要远远强于分子不规则运动导致的动量交换。所以，不能直接用Navier-Stokes方程组来计算湍流的平均运动。目前最流行的办法就是，在计算湍流的平均运动时，将Navier-Stokes方程组中的粘性系数换成一个大得多的“湍流粘性系数”，以反映湍流中非定常旋涡运动导致的动量交换效应（这就是湍流模拟中所谓的“Bousinessq湍流粘性系数假设”）。

对于文章开头的那个二维射流的例子，我们可以在后处理中显示出湍流粘性系数的分布（图5、图6）。可以看出，湍流粘性系数要比流体本身的粘性系数（μ=10-5Pa•s）大几个数量级。

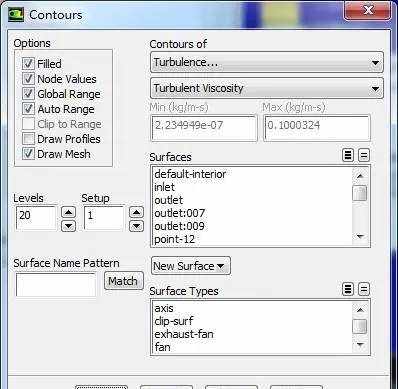
图5 显示“湍流粘性系数”

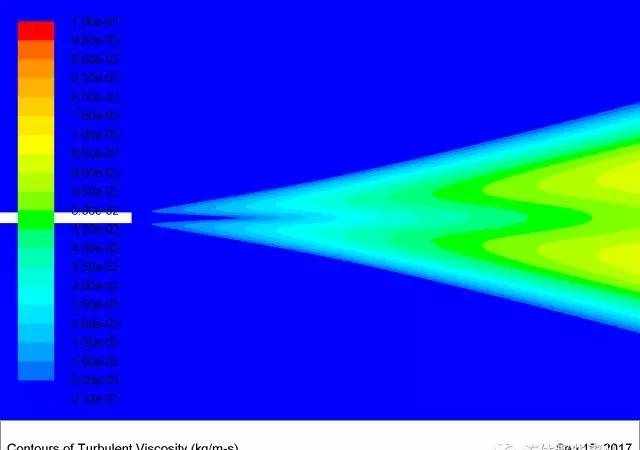
图6 湍流粘性系数的分布

如果将表1中的粘性系数换成“湍流粘性系数”μt重新计算，动量方程左边和右边的数值就很接近了（表2）。

表2 x方向动量方程左边和右边的数值。考虑湍流粘性系数

湍流模型的作用就在于计算这个“湍流粘性系数”。不同的湍流模型，如k-ε、SA、k-ω，它们的差别就在于计算湍流粘性系数的具体方法有所区别。但是，目前所有这些湍流模型都建立在某种简化假设或者经验性模型的基础之上，所以都不是十分精确，而且存在普适性差的问题。对于一个湍流模型，即使它预测某个特定的流动问题很准确，但是，如果换一个流动，也许就会误差很大。

关于上述几个湍流模型分别适用于计算哪些流动（即湍流模型的选择问题），在FLUENT的User's Guide中有详细的介绍。（在User's Guide中的“Choosing a Turbulence Model”这一节中的第一小节“Reynolds Averaged Navier-Stokes (RANS) Turbulence Models”）

感谢北京航空航天大学宇航学院的研究生田久祾。他阅读了本文的初稿并提出了很好的建议。