ARIMA ARIMA/Sarima与LSTM的时间序列数据集成学习（附链接）

这篇文章5500字左右，10+分钟。

本文讨论了简单Sarima萨里玛和LSTM时间序列数据的集成学习。

Sharmistha Chatterjee

https://towardsdatascience.com/@sharmi.chatterjee

动机

在传统的时间序列预测中，有五种最常用的时间序列模型，包括:

自回归(AR)模型；移动平均(MA)模型；自回归移动平均(ARMA)模型；自回归整合移动平均模型(ARIMA)；季节性整合自回归移动平均模型(SARIMA)模型。

自回归AR模型用以前值和当前残差线性表示时间序列的当前值，而移动平均MA模型用以前残差线性表示时间序列的当前值。

ARMA模型是AR模型和MA模型的组合，其中时间序列的当前值线性表示为它的前一个值以及当前值和前一个残差序列。AR、MA和ARMA模型中定义的时间序列都是平稳过程，即这些模型的均值与其观测值之间的协方差不随时间变化。

对于非平稳时间序列，需要将序列转化为平稳随机序列。ARIMA模型一般适用于基于ARMA模型的非平稳时间序列，其差分过程可以有效地将非平稳数据转化为平稳数据。利用季节差异和ARIMA模型相结合的SARIMA模型对具有周期性特征的时间序列数据进行建模。

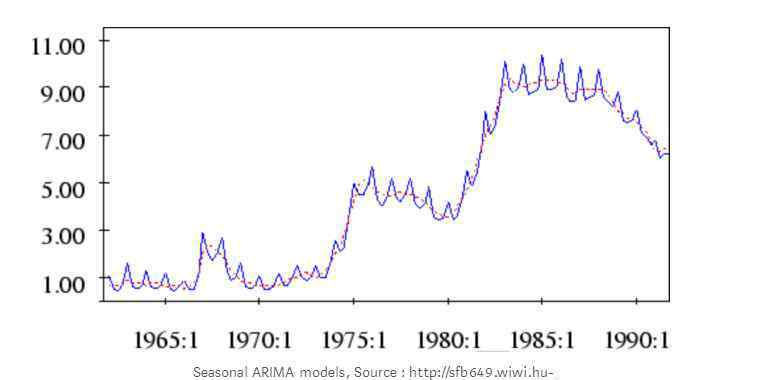
通过比较这些算法模型在时间序列上的性能，发现机器学习方法优于简单的传统方法，其中ETS模型和ARIMA模型的综合性能最好。下图是模型之间的比较。

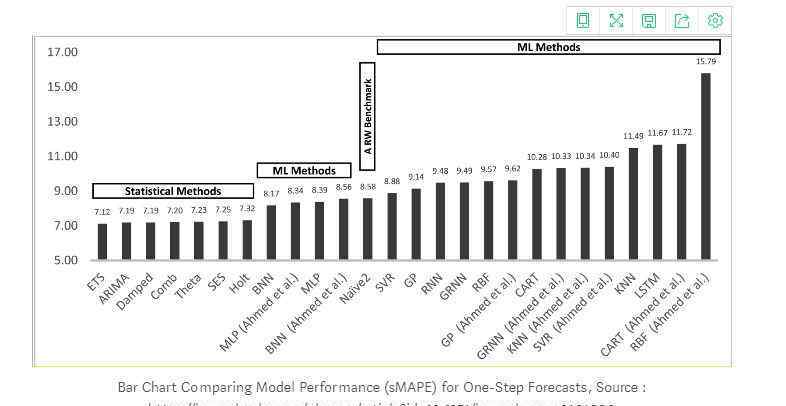
然而，除了传统的时间序列预测之外，近年来，在时间序列预测的深度学习领域，循环神经网络(RNN)和长短期记忆(LSTM)已经广泛应用于计算机视觉、自然语言处理和金融等许多学科。深度学习方法可以识别数据的结构和模式，如时间序列预测中的非线性和复杂性。

新开发的基于深度学习的时间序列数据预测算法，如“长短期记忆(LSTM)”算法，是否优于传统算法仍是一个有待研究的问题。

本文的结构如下:

了解深度学习算法RNN、LSTM以及与LSTM集成学习如何提高性能。了解传统的时间序列模型技术ARIMA，以及当它与MLP和多元线性回归相结合时，如何在集成方法中改进时间序列预测。了解使用ARIMA与LSTM的问题和场景，两者间的优劣对比。了解使用SARIMA进行时间序列建模时，如何与其他基于空间、基于决策和基于事件的模型进行集成学习。

然而，本文没有详细阐述更复杂的时间序列。比如复杂的不规则时间结构，观测值缺失，强噪声，多变量之间关系复杂。

长短期记忆网络

LSTM是一个特殊的RNN，它由一组具有特征的单元组成，用于记忆数据序列，而组中的单元用于捕获和存储数据流。此外，集合中的单元构成前一模块和当前模块之间的内部互连，从而将来自多个过去时刻的信息传输到当前模块。每个单元格中使用门来处理、过滤或添加下一个单元格中的数据。

单元中的门基于sigmoid神经网络层，使单元能够选择性地传递或丢弃数据。每个Sigmoid层输出一个介于0和1之间的数字，这是每个单元中应该传递的数据数量。更准确的说，如果这个值为0，表示“不要让任何数据通过”，如果这个值为1，表示“让所有数据通过”。为了控制每个单元的状态，每个LSTM涉及三种类型的门:

遗忘门输出一个介于0到1之间的数字，其中1表示“完全保留此值”；而0则意味着“完全忽略此值”。记忆门决定选择哪些数据通过sigmoid层和tanh层后需要存储到数据单元中。初始sigmoid层，称为“输入门层”，决定需要对哪些数值进行修改，随后，由tanh层生成可以添加到状态的新候选值的向量。输出门决定每个单元输出的内容，根据数据过滤及新增数据后数据单元的状态，输出门会输出一个数据值。

就工作原理和实施机制而言，LSTM模式比ARIMA模式提供了更多的微调选项。

LSTM在时间序列预测中的应用

发现用特定数据集训练的单个LSTM网络在其他完全不同的时间序列中可能表现不佳，因此需要严格的参数优化。由于LSTM在预测方面非常成功，研究人员采用了所谓的叠加集成方法，该方法将多个LSTM网络叠加并组合起来，以提供更准确的预测，旨在为预测问题提供更通用的模型。

通过对四种不同预测问题的研究，并根据RMSE评价量表，得出叠加LSTM网络的性能优于常规LSTM网络和ARIMA模型的结论。

通过调整每个LSTM的参数，可以提高积分方法的整体质量。单个LSTM网络性能差的原因是需要调整大量的LSTM网络参数。因此，综合LSTM网络的概念得到了发展，它减少了优化大量参数的需要，提高了预测质量，从而为预测问题提供了更好的选择。

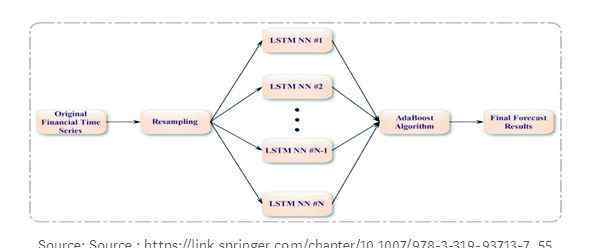
在其他集成技术中，如上图所示，具有长期短期记忆的混合集成学习(LSTM)可用于预测金融时间序列。AdaBoost算法用于组合和预测长期和短期记忆(LSTM)网络。

首先利用AdaBoost算法训练数据，从原始数据集生成替换样本，得到训练数据。然后，使用LSTM预测每个训练样本。最后，利用AdaBoost算法综合所有LSTM预测器的预测结果，生成综合结果。两个主要日汇率数据集和两个股市指数数据集的实证结果表明，AdaBoost-LSTM集成学习方法优于其他单一预测模型和集成学习方法。

AdaBoost-LSTM集成学习方法在金融时间序列数据预测中有着广阔的应用前景，对于汇率、股指等非线性、不规则的时间序列数据也有着良好的应用前景。

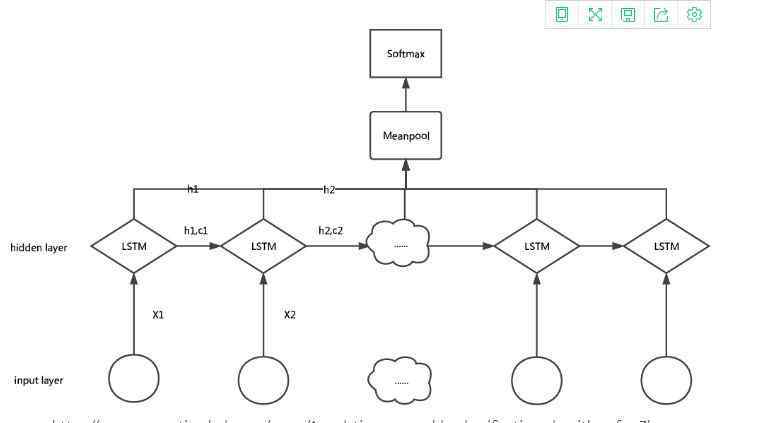
如上图所示，在LSTM集成学习的另一个例子是，当输入层包含从时间t1到tn的输入时，在每个时间的输入被输入到LSTM层，并且每个LSTM层HK的输出表示在时间k的信息的一部分，该信息被输入到输出层，并且输出层从所有接收的输出聚集和计算平均值。此外，平均值被输入到逻辑回归层以预测样本的标签。

阿里马

ARIMA算法是一种捕捉时间序列数据中时间结构的模型。然而，仅靠ARIMA模型很难对变量之间的非线性关系进行建模。

自回归综合移动平均模型(ARIMA)是自回归(AR)过程和移动平均(MA)过程相结合的广义自回归移动平均(ARMA)模型，它构造了时间序列的复合模型。

AR：自回归。一种使用一个观察和多个滞后观测之间依存关系的回归模型。I：整合。通过计算不同时间观测值的差值，使时间序列平稳化。MA：移动平均。当对滞后观测(q)使用移动平均模型时，计算观测值与残差项之间的依赖性的一种方法。阶为p的AR模型的一种简单形式，即AR(P)，可以写成一个线性过程，由以下公式表达：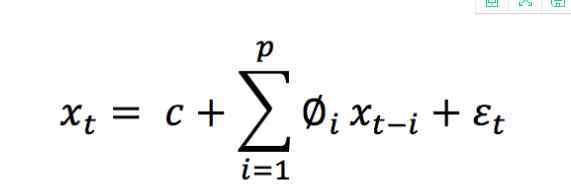

这里xt代表平稳变量，C是常数，T中的项是自相关系数，1，2，...残差p和ξt是均值和σ t方差为零的高斯白噪声序列。

ARIMA模型的一般形式表示为ARIMA(p，q，d)。对于季节性时间序列数据，短期非季节性部分可能对模型有贡献。ARIMA模型通常表示为ARIMA(p，q，d)，其中:

p是训练模型时使用的滞后观测数目（即：滞后阶数）。d是应用差分的次数(即差分的阶数)。q为移动平均窗口的大小(即移动平均的阶数)。

例如，ARIMA (5，1，0)表示自回归的滞后值设置为5，它使用一阶差分使时间序列稳定，而不考虑任何移动平均窗口(即窗口大小为零)。RMSE可以作为误差度量指标来评价模型的性能、预测的准确性和预测的准确性。

因此，我们需要使用季节性ARIMA模型，这是一个包含非季节性和季节性因素的复合模型。季节性ARIMA模型的一般形式表示为(P，Q，d) X (P，Q，D)S，其中P为非季节性AR阶，D为非季节性差异，Q为非季节性MA阶，P为季节性AR阶，D为季节性差异，Q为季节性MA阶，S为重复季节性模式的时间跨度。预测季节ARIMA模型最重要的一步是确定(p，q，d)和(p，q，d)的值。

根据数据的时间图，如果方差随时间增加，应采用方差平滑变换和差分法。

自相关函数(ACF)用于计算由P个时延分隔的时间序列中观测值之间的线性相关，偏自相关函数(PACF)用于确定需要多少个自回归项Q，逆自相关函数(IACF)用于检测差值，进而可以得到自回归阶P和差阶D、移动平均阶Q及其对应的季节参数P、D、Q的初始值。参数d是非平稳时间序列到平稳时间序列的差频变化顺序。

在对单个时间序列数据使用单变量自回归移动平均(ARMA)方法的过程中，自回归(AR)模型与移动平均模型(MA)相结合，单变量“差分自回归移动平均模型(ARIMA)”是一种特殊的考虑了差分的ARMA模型。

多元ARIMA模型和向量自回归模型是另外两种流行的预测模型，它们通过考虑多个进化变量来推广单变量ARIMA模型和单变量自回归模型。

ARIMA是一种基于线性回归的预测方法，最适合单步样本预测。这里提到的算法是多步样本预测和重新估计，即每次对模型进行重新拟合，建立最佳的估计模型。该算法基于输入的“时间序列”数据集，建立预测模型，计算预测的均方误差。它存储了两个数据结构来保存每次迭代中累积添加的训练数据集，即用于测试数据集连续预测的“历史”值和“预测”值。

基于ARIMA的综合学习

分别对ARIMA、MLP和多元线性回归预测模型进行训练、验证和检验，得到目标污染物浓度预测值。为了训练和拟合ARIMA模型，利用自相关函数(ACF)和偏自相关函数(PACF)来估计P、D和Q的值。MLP模型是用以下参数建立的:用于权重优化的解算器是lbfgs，因为它可以更快地收敛，并且对于较少维度的数据具有更好的性能。

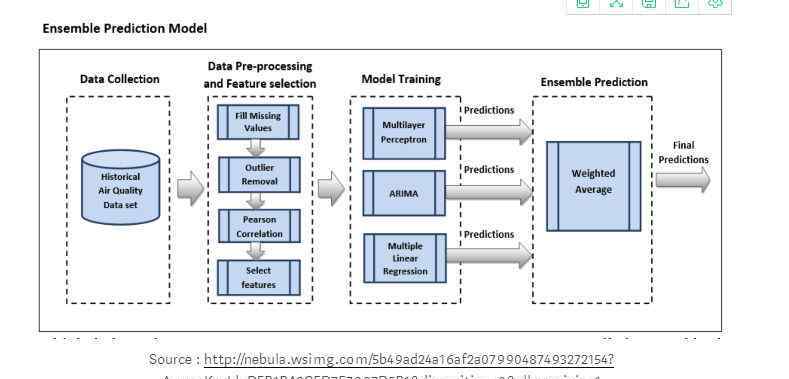
与随机梯度下降优化器相比，它得到了更好的结果。它使用激活函数“RELU”来表示修改后的线性元素(relu)函数，从而避免了梯度消失的问题。然后，利用加权平均集成技术将各模型的预测合并成最终预测。加权平均集将每个模型的预测乘以权重，然后计算其平均值。每个基本模型的权重可以根据每个模型的性能进行调整。

通过加权平均技术对各模型的预测进行组合，其中各模型根据其性能被赋予不同的权重，性能较好的模型被赋予较高的权重。权重分配原则要保证权重之和必须等于1。

自回归移动平均法

ARIMA是单变量时间序列数据最广泛使用的预测方法之一，但它不支持带有季节性成分的时间序列。为了支持序列的季节组成部分，ARIMA模型被扩展到沙里马。SARIMA(季节性差异自回归移动平均模型)应用于包含趋势和季节性的单变量数据，SARIMA由一系列趋势和季节性元素组成。

与ARIMA模型相同的一些参数是:

p:趋势的自回归阶数。d:趋势差分阶数。q:趋势的移动平均阶数

不属于ARIMA的四个季节因素是:

P:季节性自回归阶数。D:季节性差分阶数。Q:：季节性移动平均阶数。m:单个季节性周期的时间步长数。

萨里玛模型可以定义为:

SARIMA (p，D，q) (P，D，Q) m

如果m为12，则指定每年的季节周期为月数据。

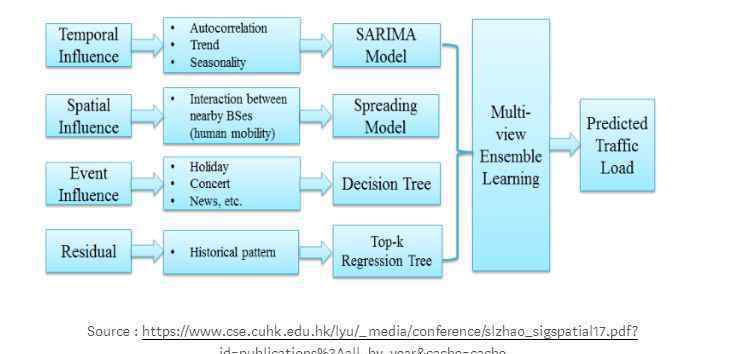
SARIMA时间序列模型也可以与基于空和事件的模型相结合，生成解决多维ML问题的集成模型。该模型可用于预测一年中不同时间蜂窝网络中的小区负载，如下图所示。

时间序列分析中的自相关性、趋势性和季节性(工作日和周末效应)可以用来解释时间影响。

区域和小区的负载分布可用于预测不同时间间隔内的稀疏和过载小区。

使用决策树预测事件(节假日、特殊群体集会和其他活动)。

数据集、问题和模型的选择

在分析经典机器学习和深度学习机制需要解决的问题时，在最终选择正确的模型之前，应该考虑以下因素。

经典时间序列模型(ARIMA/SARIMA)和深度学习模型性能指标的不同。模式选择所生成的业务影响是长期的还是短期的。更为复杂模型的设计、实现和维护成本。损失的可解释性。

首先，数据是高度动态的，往往很难梳理出时间序列数据的嵌入结构；其次，时间序列数据可以是非线性的，并且包含高度复杂的自相关结构。不同时间段的数据点可以进行相关和线性近似，有时数据中的所有结构都无法建模。传统的方法，如自回归模型，试图估计模型的参数，这可以被视为生成数据结构的平滑逼近。

综上所述，ARIMA用来建立线性关系的模型数据更好，而RNN(依赖于激活函数)用来建立非线性关系的模型数据更好。ARIMA模型为数据科学家提供了更好的选择。之后，当李氏、怀特和格兰杰(LWG)检验后的数据的残差仍然包含非线性关系时，可以用RNN等非线性模型进一步处理数据集。

将LSTM和ARIMA应用于一组金融数据后，结果表明LSTM优于ARIMA，LSTM算法的预测精度比ARIMA平均提高了85%。

结论

最后给出了一些案例分析。为什么某些机器学习方法在实践中表现不好，但在人工智能的其他领域却表现很好？因此，本文评价了SARIMA萨里玛模型和LSTM模型性能不佳的原因，并设计了一种提高模型性能和精度的机制。这些模型的应用领域和性能如下:

ARIMA对短期预测有较好的预测效果，而LSTM对长期模型有较好的预测效果。传统的时间序列预测方法(ARIMA)侧重于具有线性关系和固定人工诊断时间依赖的单变量数据。对大量数据集的机器学习问题研究发现，与ARIMA相比，LSTM获得的平均错误率在84-87%之间，表明LSTM优于ARIMA。深度学习中的“epoch”为训练次数，它对训练预测模型的性能没有影响，呈现出真正的随机性。LSTM与RNN和MLP等更简单的NNS相比，似乎更适合于拟合或过度拟合训练数据集，而不是预测数据集。具有庞大数据集的神经网络(LSTMS和其他深度学习方法)提供了将其分成几个较小的批次并在多个阶段进行训练的方法。批大小/每个块大小根据使用的培训数据总数来定。术语：迭代，用于表示完成整个数据集模型训练所需的批次数。LSTM无疑更为复杂，训练难度较大，在大多数情况下其性能不会超过简单ARIMA模型的性能。传统的方法，如ETS和ARIMA，适用于一元数据集的单步预测。像Theta和Arima这样的经典方法在单变量数据集的多步预测方面表现出色。像ARIMA这样的经典方法侧重于固定的时间依赖性：不同时间观测值之间的相互关系，这就需要分析和说明作为输入的滞后观测值的数量。机器学习和深度学习方法尚未实现其对单变量时间序列预测的承诺，这方面还有许多研究要做。神经网络增加了处理噪声和非线性关系的能力，并具备任意定义且有固定数量的输入。此外，NNS可输出多变量和多步预测。递归神经网络(RNNs)增加了有序观测的显式处理，并能够从上下文中学习时间依赖关系。通过从一定时间内对序列的一次观测值，RNN可以学习到该序列先前所的相关观测，并对后续相关性进行预测。当LSTMS用于学习长期序列中的相关性时，在无需指定任何时间窗口的情况下， 它可以对复杂的多变量序列建模。

引用

1.https://journals.plos.org/plosone/article? id = 10.1371/journal . pone . 0194889

2.https://machine learning master . com/discovery-comparison-classic-and-machine-learning-methods-for-time-series-prediction/

3.https://arxiv.org/pdf/1803.06386.pdf

4.https://pdf . semantic scholar . org/e58c/7343 ea 25d 05 F6 d 859d 66d 6b B7 FB 91 EC F9 C2 f . pdf

5.用于鲁棒时间序列预测的集成递归神经网络，作者:S.Krstanovic和H.Paulheim，发表于《人工智能》第34期，由M.Bramer和M.Petridis编辑，斯普林格国际出版社，2017年，第34-46页，ISBN: 978-3-319

6.https://link . springer . com/chapter/10.1007/978-3-319-93713-7 _ 55

7. http://nebula.wsimg.com/5b49ad24a16af2a07990487493272154?AccessKeyId=DFB1BA3CED7E7997D5B1&disposition=0&alloworigin=17.http://nebula.wsimg.com/5b49ad24a16af2a07990487493272154?接入密钥id = DFB1 ba 3 ced 7e 7997 D5 B1 & amp；处置= 0 & ampalloworigin=1

8.https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3641111/

9.基于节能蜂窝网络的流量预测:一种机器学习方法

https://www . CSE . cuhk . edu . hk/lyu/_ media/conference/slzhao _ sigspatial 17 . pdf？id = publications % 3 all _ by _ year & amp；缓存=缓存

利用时间序列数据的集成学习洞察力的SARIMA萨里玛vs LSTM

https://towards data sciences . com/ARIMA-sarima-vs-lstm-with-ensemble-learning-insights-for-time-series-data-509 a5d 87 f20a

译者简介:陈智言毕业于北京交通大学，通信与控制工程硕士。曾任长城计算机软件系统公司工程师、大唐微电子公司工程师。现任北京武夷超群科技有限公司技术支持..目前从事智能翻译教学系统的运维工作，在人工智能深度学习和自然语言处理(NLP)方面积累了一定的经验。

本文转自:数据学校thu被授权；

结束