卡尔曼滤波器 卡尔曼滤波器的工作原理（一）

可以说卡尔曼滤波器非常神奇，因为它是一种在不确定条件下组合信息的通用而强大的工具。有时它提取准确信息的能力几乎是惊人的。

视频演示了卡尔曼滤波器通过测量自由漂浮物体的速度来计算其方向。

1.什么是卡尔曼滤波器？

卡尔曼滤波器可以用于某些动态系统的任何不确定信息，它可以对系统下一步的工作做出明智的预测。即使出现杂乱的动作，干扰预测的干净动作，卡尔曼滤波器往往也能很好地计算出实际的动作。这可能是因为它可以利用一些不可思议的现象之间的相关性！

卡尔曼滤波器是连续变化系统的理想选择。卡尔曼滤波器具有内存占用小、运算速度快、适合实时处理和嵌入式系统等优点。

Google搜索找到的实现卡尔曼滤波的数学描述一般都很模糊。这真的很糟糕，因为如果你用正确的方式来看，卡尔曼滤波器其实超级容易理解。所以，是一个很好的话题。在这里，我们尝试用清晰优美的图片和颜色来解释卡尔曼滤波器。读这篇文章的条件很简单，需要的只是对概率和矩阵的基本理解。先说一个卡尔曼滤波可以解决的简单例子。

2.卡尔曼滤波器能做什么？

举一个有趣的例子:如果你有一个可以在森林里行走的小机器人，那么机器人必须准确知道它在哪里，这样它才能导航。

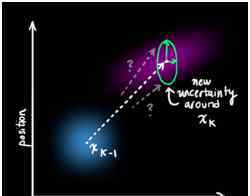
.接下来，需要一些方法来观察当前状态并及时预测下一个状态。注意，我们不知道哪个状态是“真”，但是预测函数并不关心这个，它只是对所有信息起作用，并提供一个新的分布:

虽然有一个预测矩阵可以用来表示下一个状态，但是我们仍然不知道如何更新协方差矩阵。所以我们需要用另一个公式。如果我们用矩阵乘以分布中的每个点，它的协方差矩阵会发生什么变化？很简单，可以得到下面的等式:

5.外部影响

然而，我们不能捕捉一切。可能会有一些与状态本身无关的变化，即外部因素可能会影响系统。例如，当状态模拟列车的运动时，列车驾驶员可能会踩下加速器，导致列车加速。类似地，在上述机器人示例中，导航软件可以发出转动轮子或停止的命令。如果我们知道外界发生的事情的信息，我们可以把它引入到一个名为的向量中，然后把它作为一个修正引入到预测过程中。假设由于油门设定或控制指令导致的预期加速度a是已知的。从基本运动学来看:

6.外部不确定性

如果国家根据自己的特点发展，一切都好。如果外部因素发展，只要知道这些外部因素是什么，一切还是好的。

但是我们不知道的外部因素呢？比如跟踪一架四翼直升机，很可能会受到风的影响。如果你跟随轮式机器人，轮子可能会打滑，或者地面碰撞可能会变慢。如果这些情况发生，我们无法实现目标跟踪和预测，因为我们没有考虑这些额外的因素。我们可以通过在每个预测步骤后添加一些新的不确定性来模拟与外部因素相关的不确定性。

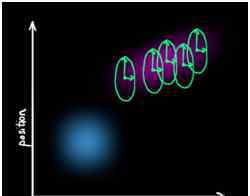
在此过程中，会生成一个具有不同协方差的新高斯光斑:

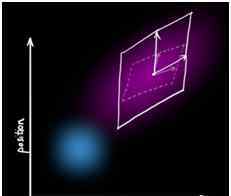
未完待续。。。。

感谢文博士提供的资料！

欢迎关注！转载请注明出处！