摩纳哥蒙特卡洛 详解蒙特卡洛方法：这些数学你搞懂了吗？

机心编译

参与:熊猫

加州大学洛杉矶分校计算机科学专业的章瑞平最近开始在他的博客上连载关于强化学习的文章。这些文章主要基于理查德·萨顿和安德鲁·巴尔托合著的《强化学习:导论》，并增加了一些例子来说明。本系列文章介绍了赌博机问题、马尔可夫决策过程和蒙特卡罗方法。本文是蒙特卡罗方法的汇编。更多相关文章及最新更新可登陆https://https://one raynyday . github . io

目录

1.目录

2.正式介绍

first-visit 蒙特卡洛

3.蒙特卡罗作用值

4.蒙特卡罗控制

探索开始在策略：ϵ-贪婪策略ϵ-贪婪收敛离策略：重要度采样离策略标记法普通重要度采样加权重要度采样增量实现其它：可感知折扣的重要度采样其它：预奖励重要度采样

5.用Python实现的策略内模型

示例：Blackjack示例：Cliff Walking

6.总结

我们讨论了马尔可夫决策过程(MDP，见https://goo.gl/wVotRL)和寻找行动成本函数的最优和

的算法。我们使用策略迭代和值迭代来求解最优策略。

强化学习有一个动态规划的解决方案是好的，但是也有很多局限性。比如，关于状态转移的概率，你知道的现实世界的问题有很多吗？可以从一开始的任何状态开始吗？你的MDP有限公司吗？

然后，我想你会很高兴知道蒙特卡洛方法。这是一个经典的方法，可以逼近困难的概率分布，可以解决你对动态规划解的所有担心！

同理，我们会根据理查德·萨顿的精读教材《强化学习:导论》进行讲解，并给出一些本书没有的补充说明和例子。

向前

蒙特卡洛模拟以摩纳哥的赌场命名。因为概率和随机结果是这种建模技术的核心，就像轮盘、骰子、老虎机一样。

与动态规划相比，蒙特卡罗方法将以一种新的方式看待问题。问题是:我需要从环境中获得多少样本才能区分好策略和坏策略？

这时，我们需要重新引入“回报”的概念，指的是长期经营的预期收益:

有时，如果epic有一个持续有限时间的非零概率，那么我们将使用一个折扣因子:

而不是。简单的把G[s]换成G[s，a]好像很合适，确实如此。一个很明显的问题是，现在我们已经从S 空变成了S×A 空，会大很多，还需要对其进行采样，才能找到每个状态-动作元组的期望收益。

另一个问题是，随着搜索空的增加，如果我们在策略上变得太快贪婪，我们越来越有可能无法探索所有的状态-动作对。我们需要把勘探和开发适当地结合起来。我将在下一节解释我们克服这个问题的方法。

蒙特卡罗控制

回想一下马尔可夫决策过程中的策略迭代。这种情况没有太大区别。我们仍然固定我们的π，寻找它，然后找到一个新的π’并继续。一般过程是这样的:

行动。

现在我们的问题是:这个会收敛到蒙特卡罗方法的最优π吗？答案是:会收敛，但不会收敛到那个策略。

-贪婪收敛

我们从q和一个贪婪策略π'(s)开始。

，那么

是什么样的？换句话说，你是如何利用你从采样B得到的信息来确定从π得到的预期结果的？

你可以直观的想一想:“如果B多次选择A，π多次选择A，那么B的行为应该是决定π行为的重要因素。反过来说，“如果B多次选择A，π从来不选择A，那么B在A上的行为应该和π在A上的行为没有任何关系”也有道理吧？

这几乎就是重要抽样率的意思。给定一条轨迹，当给定策略π时，该精确轨迹的概率为:

极好的估计。最基本的方法是使用一种叫做普通重要性抽样的技术。假设我们有n集样本:

当然，这可以很容易地概括为一种每次访问的方法，但我只想呈现最简单的形式，了解要点。也就是说，我们需要用不同的方式对每一部史诗的回归进行加权，因为对于π来说，更可能发生的轨迹应该比永远不会发生的轨迹有更大的权重。

重要抽样法是一种无偏估计量，但它有极端方差问题的困扰。假设一部kth史诗的重要度比为1000。这个比例很大，但是绝对有可能。这是不是意味着奖励一定要多1000倍？如果我们只有一部史诗，我们的估计会是这样的。在长期操作中，因为我们有乘法关系，这个比值可能会爆炸，也可能会消失。这对于估计的目的来说有点问题。

3).加权重要性抽样

为了减少方差，通过除以所有重要比率的幅度总和(有点类似于softmax函数)来减少估计幅度是一种简单而直观的方法:

就是我们的体重。

我们希望基于

建造

，这很可行。使用

说，我们可以不断更新运行总和，即:

的更新规则非常明显:

世界上也可以应用一个非常相似的类比。

我们在更新价值函数的时候，也可以更新我们的策略π。我们可以用旧的，好用的来更新我们的π。

警告:前面有很多数学。目前现有的资料其实已经足够，但接下来的介绍会让我们更接近现代的研究课题。

5).其他:感知折扣的重要性抽样

到目前为止，我们已经计算了回报，并对回报进行了采样，以获得我们的估计。但是我们忽略了g的内部结构，它实际上只是折扣奖励的总和，不能整合到我们的比率ρ中。一个折扣感知重要性抽样模型γ是一种终止概率，即一个epic在某个时间步长t终止的概率，所以它一定是一个几何分布geo (γ):

而完全收益可以看作是对随机变量的随机数的期望:

您可以按如下方式构造任意伸缩和:

综上所述，我们可以看到对于从x开始的k，我们有。

换成g:

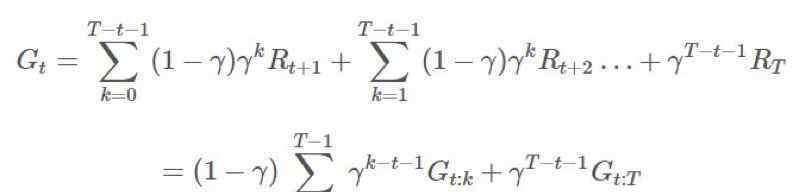
这将导致1，γ，γ2项的等效系数。这意味着我们现在可以将其分解为不同的部分，并对重要抽样率进行折扣。

现在回想起来，我们有:

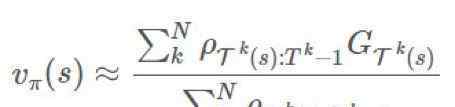
在这个例子中，我们使用了OpenAI的健身房。在这里，我们使用一个腐朽-贪婪策略来解决21点。

importgym健身房

env =健身房. make(" 21点-v0 ")

#典型的进口

importgym健身房

importnumpy asnp

importmatplotlib.pyplot asplt

fromcimportfinitemcmodel AsMC

eps = 1000000

S = [(x，y，z) forx inrange( 4，22) fory inrange( 1，11) forz in[True，False]]

A = 2

m = MC(S，A，ε= 1)

fori inrange( 1，eps+ 1):

ep = []

observation = env.reset()

同时:

#选择行为策略

action = m.choose_action(m.b，observation)

#运行模拟

next_observation，悬赏，done，_ = env.step(action)

ep.append((观察、行动、奖励))

观察=下一次观察

ifdone:

打破

m.update_Q(ep)

#衰减ε，达到最优策略

m .ε=最大值((eps-i)/eps，0.1)

打印(“最终预期回报:{}”。格式(m.score(env，m.pi，n_samples= 10000)))

#绘制3D线框，如示例mplot3d/wire3d_demo所示

X = np.arange( 4，21)

Y = np.arange( 1，10)

Z = np.array([np.array([m.Q[(x，y，False)][ 0] forx inX]) fory inY])

X，Y = np.meshgrid(X，Y)

from mpl _ toolkits . mplot 3d . axes 3d importaxes 3d

图= plt.figure()

ax = fig.add_subplot( 111，投影= '3d ')

ax.plot _线框(X，Y，Z，rstride= 1，cstride= 1)

ax.set_xlabel(“玩家之手”)

ax.set_ylabel(“经销商之手”)

ax.set_zlabel(“返回”)

PLT . save fig(" blackjack policy . png "/>

我也写过这个模型的快速离场策略版本，但是还需要完善，因为我只是想得到一个性能基准。结果如下:

迭代:100/1k/10k/100k/100万。

在10k样本上测试预期回报。

政策上:贪婪

-0.1636

-0.1063

-0.0648

-0.0458

-0.0312

政策上:EPS-贪婪witheps= 0.3

-0.2152

-0.1774

-0.1248

-0.1268

-0.1148

非政策加权重要性抽样:

-0.2393

-0.1347

-0.1176

-0.0813

-0.072

因此，从策略的重要性来看，抽样可能更难收敛，但最终结果比贪婪策略要好。

例子:悬崖漫步

所需的代码修改其实很小，因为我之前提到过，蒙特卡洛采样受环境影响很小。我们只需要修改代码的这一部分(不包括绘图部分):

#之前:21点-v0

env = gym . make(" CliffWashing-v0 ")

# Before: [(x，y，z) forx inrange( 4，22) fory inrange( 1，11) forz in[True，False]]

S = 4* 12

#之前:2

A = 4

然后我们跑这个健身房，Eπ(G)，拿-17.0。还不错！在悬崖行走问题中，一张地图中有些模块是悬崖，有些是平台。每走一步，在平台上行走的奖励为-1，掉下悬崖的奖励为-100。无论何时你走在悬崖模块上，你都应该回到起始位置。这么大的地图，每一个epic-17.0都接近最优策略。

总结

对于任何具有“奇怪”动作或观察空概率分布的任务，蒙特卡罗方法是计算最优值函数和动作值的一种非常好的技术。以后我们会介绍一个更好的蒙特卡洛方法的变体，但这篇文章也可以为你的强化学习提供很好的基础知识。

原文链接:https://one raynyday . github . io/ml/2018/05/24/rewarding-learning-Monte-Carlo/

[特殊团体购买]

加入义山商人俱乐部社区，给韩旭老师做演讲

社区服务内容:

回答问题。您的交易问题将由资深交易员实时回答。

交易计划:每天下午在集团内公布一山系统次日交易分析计划。

场内指导，交易日实时解读强弱品种，提示交易机会。

报价提示，共同捕捉优秀的交易机会，提示止损位、目标和主观获利机会。

导师讲课。宜山操盘手俱乐部韩旭老师会不定期与群友分享宜山交易系统的精髓。大家可以免费学习。

同学们分享，偶尔邀请宜山团队的优秀交易员与团友分享自己的实践经验。

线下沙龙，时不时组织团体聚会，牛人面对面分享干货。

成本:原价199元，现价99元