迪杰斯特拉算法 【论文精选】Dijkstra算法的并行实现

裴淑玲、王

研究了多核架构下基于OpenMP的Dijkstra并行算法，设计了基于Dijkstra算法的并行程序。对传统的Dijkstra算法进行分析，定义优化方向，然后利用OpenMP开发工具对并行程序进行优化调试。结果表明，本文算法操作简单，充分利用了多核处理器并行计算的优势，提高了算法的运行效率，验证了算法的优越性。

关键词:多核；Dijkstra算法；OpenMP并行算法

中国图书馆分类号:TP312文献识别码:adoi:10.19358/j . ISSN . 1674-7720 . 2017 . 09 . 008

引用格式:裴淑玲，王。Dijkstra算法的并行实现[J]。微机与应用，2017，36 (9): 25-27。

0简介

随着多核技术的发展，串行执行程序的缺点暴露出来。传统的Dijkstra算法是串行算法，搜索过程简单易懂，程序设计简单。然而，大量的内存空和计算时间的开销成为该算法的瓶颈，有效的解决方案之一就是并行计算。为了最大化计算能力，一个应用程序需要划分成几个相对独立的任务，交给几个计算内核执行。为了直接从语言组件支持并行性，摆脱串行语言的约束，设计了一种新的编程模型。与传统算法相比，该并行算法能够更有效地提高运行效率，充分发挥高性能多核处理器的功效。

1便士

OpenMP是支持跨平台内存共享的多线程并发编程模型。它在开发过程中不需要考虑数据分布，具有良好的可移植性和可扩展性。它还支持C、C++和FORTRAN语言。OpenMP提供了一系列的架构和编程平台，建立了简洁高效的编程指令命令和并行编程方法，为各种串行程序的并行化提供了可行的方案。OpenMP不是一种独立的并行语言，它通过在适当的位置添加编译指令和运行库函数来并行化串行程序。OpenMP从主线程开始，一直串联执行线程。当线程的某些点需要并行执行时，程序派生出额外的线程来形成一个线程组。这些线程在并行域的代码区并行执行。当线程到达整个并行区域的末尾时，它们等待直到整个线程组到达并最终连接。此时，只有主线程继续执行，直到下一个并行区域或程序[2]结束。示例[3]:

int main(int argc，char*argv[]){

#pragma omp并行

for(int I = 0；i<。10;i++)

{

printf("i=%d/n "，I)；

}

printf(" finished . n ")；

返回0；

}

在该程序中，使用OpenMP编译指令“#pragma omp parallel for”并行执行for循环的内容，提高了效率。

二维最短路径算法

2.1算法思路

Dijkstra算法是典型的单源最短路径，从起点向终点向外扩展。假设Len(v)表示从一个顶点到给定顶点u的最短距离，w(u，v)表示两个顶点之间的距离。给两个顶点V1和V2，找出它们之间的最短距离。算法描述如下[4]:

(1)给定顶点V1，标记该顶点并初始化所有顶点，并将顶点V1放入集合S..

(2)对于集合S中的所有顶点Vi，计算与Vi相邻的所有顶点Uj的MD (UI，Vi) = W (UI，VJ)+Len (VJ)值，找出md(u，v)值最小的顶点U，将顶点U放入集合S中..

(3)重复上述步骤，直到将目标顶点V2放入集合S中，就可以得到顶点V1和V2之间的最短距离，就可以得到最短路径[5]。

Dijkstra最短路径算法流程图如图1 [4]所示。

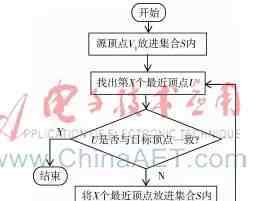
2.2算法分析

通过对算法的分析，得出了算法的不足之处。在每次迭代中，未标记的节点以无序的形式存储在数组或链表中。每次选择最短路径节点时，所有未标记的节点都必须扫描一次。当节点数较大时，这将成为制约计算速度的关键因素。

基于OpenMP的3并行Dijkstra算法

3.1算法的并行化

编程时，代码的并行执行并不局限于某个函数的并行化，还需要在函数内部创建线程，使关键计算并行执行。频繁的线程创建会增加开销[6]。OpenMP可以有效地并行化程序，解决多核编程中的线程创建问题。

(1)Dijkstra并行算法设计思想

从Dijkstra的最短路径算法可以看出，集合S每次迭代后不动点个数都会增加1，每次迭代都依赖于上一次迭代的结果，循环之间存在依赖关系，因此不能直接并行化外循环[7]，因此提出了内循环的并行化。每个线程计算一个顶点的所有边，获得最小边并存储在一个数组的不同位置，然后从数组中找到最小值，得到距离最近的顶点[8]。继续执行外循环，直到找到最近的距离顶点和目标节点。

(2)并行算法编程流程图[4]如图2所示。

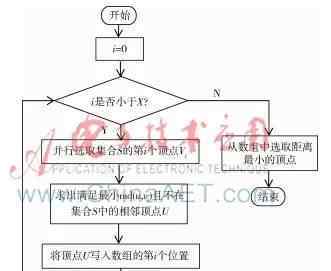
3.2并行算法的设计与实现

Dijkstra算法的并行化由两部分实现:Parallel _ GetShort-EstPath()函数实现主算法流程，SearchNextVertex()函数实现并行计算mth最近顶点的算法流程[9]。并行算法的实现代码如下[4]:

#pragma omp并行

num _ thread(p graph ->;nodecount，MIN_ITERATOR_NUM))

for(I = 0；i<。pGraph>。nnodoecount；i++)

{

pGraph>。ppNodeArray[i]->;nma gic =-1；/*被初始化为-1，这意味着没有计算最短路径的总距离*/

pGraph>。ppNodeArray[i]->;pMagic = NULL/*指针为空*/

}

PPS node[0]= pSrcNode；

ppSNode[0]->nma gic = 0；/*被初始化为0*/

ppSNode[0]->pMagic = NULL

for(x = 1；x<。pGraph>。nnodoecount；X++)/*x从1开始循环执行*/

{

DISTANCE nTotalDis

GRAPHNODE * pTNode

pTNode = NULL

NTotalDisGRAPH _ MAX _ DISTANCE

SearchNextVertex(pGraph，ppSNode，x，ppNode，pnDis)；

INT index =-1；

for(I = 0；i<。x；i++)

{

if(nTotalDis > 1；pnDis[i])

{

nTotalDis = pnDis[I]；

index = I；

}

}

if(index！=-1)

{

ptNode = PPNode[index * 2]；

pTNode>。nMagic = nTotalDis

pTNode>。pm agic = PPNode[index * 2+1]；

if(pTNode==pTagNode)

{

nTagDis = nTotalDis/*计算从源节点到目标节点的最短路径*/

打破；

}

}

否则{ /*最短路径始终存在，不应在此执行*/

打破；

}

PPS node[x]= pt node；

}

免费(PPNode)；

免费(PNDIs)；

免费(PPSnode)；

返回nTagDis/*返回从目标节点到源节点的最短路径*/

}

4实验和结果分析

为了验证并行Dijkstra算法的性能，设计了实验进行验证。采用传统的Dijkstra算法和并行化的Dijkstra算法进行实验，分析比较不同节点数和弧段下的运行时间，评价并行化性能[10]。结果如表1所示。

从表1可以看出，在执行节点数和弧段数相同的情况下，并行Dijkstra算法比串行Dijkstra算法更节省时间，运行速度大大提高。

5结论

本文对传统的Dijkstra算法进行了分析。为了节省计算机内存空和提高运算效率，在OpenMP模型下研究了Dijkstra算法的并行设计。通过数据采集和分析，验证了并行Dijkstra算法的性能。结果表明，并行算法比传统算法能更有效地提高运算效率，充分发挥高性能多核处理器的功效。

引用

，吴。引用该论文王志平，王志平，王志平.计算机科学，2012，39(5):223-228。

王志广、王兴会、李燕。引用该论文王志平，王志平，王志平.内蒙古师范大学学报(自然科学版)，2012，41(2):195-200。

彭、、顾炳根、李。引用该论文王志平，王志平，王志平.硅谷，2010，(16):97-98。

周伟明。多核计算与编程[M]。武汉:华中科技大学出版社，2009。

龚相健、邹、胡。引用该论文王志平，王志平，王志平.南华大学学报(自然科学版)，2013，27(1):64-68。

叶、王一磊。引用该论文王志平，王志平，王志平.计算机应用与软件，2011，28 (9): 272274。

李健。引用该论文王志平，王志平，王志平.渭南师范学院学报，2009，24 (5): 6164。

季慧峰，徐爱红，隋大伟。引用该论文王志平，王志平，王志平.辽宁工业大学学报(自然科学版)，2008，27(S1):222-223。

任小溪，唐玲，杰森。基于OpenMP多线程的动态负载均衡技术研究[J]。《世界科学技术研究与发展》，2008，30(3):281-285。

，黄。引用该论文王志平，王志平，王志平，王志平.计算机科学，2012，39 (10): 245-247，257。