转自:爱智慧哲学
对哲学花园的认知
西方文化中的绘画与数学透视
莫里斯·克莱因
编者按:
本文摘自莫里斯·克莱因《西方文化中的数学》第十章“绘画与透视”。数学和艺术有各种各样的联系。数学本身被认为是一门以美为灵感的艺术。数学通常可以在艺术中呈现,被人感知,比如音乐、舞蹈、绘画、建筑、雕塑、纺织。正如大卫·希尔伯特在1900年国际数学大会上的演讲中所说,“数学是所有关于自然现象的严格知识的基础”。至于绘画艺术,它通过图形、构图等美学方法来表达思想和意义,它的基础仍然离不开数学。
“列奥纳多·达·芬奇确信‘欣赏我作品的人都不是数学家。’他坚持认为绘画的目的是再现自然,绘画的价值在于它的准确再现。即使是纯粹的抽象创造,如果能存在于自然界,也必然会出现。因此,绘画是一门科学,它和所有其他科学一样,是以数学为基础的。除非通过数学表达和数学证明开辟自己的道路,否则人类的任何探究活动都不能被称为科学。再者,‘一个人如果怀疑数学的极端可靠性,就会陷入混乱,永远无法平息科学中的诡辩,只会导致空的空谈和毫无结果的争论’。"
绘画和对自然的透视,在永恒的意识中,
记录了自然的思想;在无处不在的寺庙里,
自然的真实形象被描绘出来,自然是美丽的
画面充满了巨大的宇宙。
T.坎帕内拉(坎帕内拉)
中世纪的大多数绘画都是为教堂画装饰品,主要是通过描绘的形象来表达基督教的教义和思想。这一时期结束时,画家和其他欧洲思想家一样,开始对自然感兴趣。文艺复兴时期的艺术家受到强调人和人周围的宇宙的新概念的启发,敢于面对自然,研究自然,探索自然,真实地描述自然。画家们在生机勃勃的世界里复活了瑰丽宜人的本质,重绘了美丽的图画,被证明是物质世界的幸福,是满足自然需求的不可剥夺的权利,是大地、空气、江河、海洋带来的欢乐。
在描述现实世界时,文艺复兴时期的画家对数学感兴趣有几个原因。第一个原因任何时候的作品,都是艺术家追求写实的绘画创作。没有色彩和创作意图,画家在画布上画的是一个位于空之间的几何形状。处理这些理想化的物体所使用的语言,它们所具有的理想比例,以及它们在空中的位置关系,都需要用到欧氏几何,这样这些方面才能有机地结合起来。艺术家需要的只是运用这些知识。文艺复兴时期的艺术家转向数学,不仅因为他们试图逼真地再现自然,还因为他们受到复兴的希腊哲学的影响。他们完全熟悉并充满了这样的信念:数学是现实世界的本质,宇宙是有序的,可以根据几何明确地合理化。因此,他们和希腊哲学家一样,认为要通过现象来理解本质,即需要在画布上表现自己的题材的现实性,最终要解决的问题必须与一定的数学内容有关。艺术家试图在作品中发现数学本质的最有趣的论点可以在达芬奇对比例的研究中找到。在这项研究中,他试图使理想图形的结构适应理想图形——正方形和圆形(图6)。
数学是现实的本质这一哲学观点,只是文艺复兴时期的艺术家寻求使用数学的两个原因。除此之外还有其他原因。中世纪晚期和文艺复兴时期的艺术家也是他们那个时代的建筑师和工程师,所以他们必然热爱数学。商人、世俗王子、教会人士把所有的建筑问题都交给艺术家。艺术家设计和建造教堂、医院、宫殿、修道院、桥梁、堡垒、水闸、运河、城墙和战争设备。在达芬奇的笔记中,可以找到大量这样设计的图画。他不仅作为建筑师、雕塑家、画家,还作为工程师,亲自为米兰的统治者洛多维科索夫扎服务。艺术家甚至被邀请来解决炮兵部队中炮弹的运行问题。在当时,解决这样的问题需要深厚的数学知识。文艺复兴时期的艺术家是最优秀的实用数学家,在15世纪,他们也是最博学多才的理论数学家。这样说一点也不夸张。
激发文艺复兴时期艺术家数学天才的特殊问题,也是我们这里要讨论的问题,就是如何在二维画布上描绘现实中的三维风景。艺术家通过创造一个全新的数学视角理论体系,解决了这个问题,进而创造了一种新的绘画风格。
在整个绘画史上,用于在石膏模板和画布上绘制图案的各种方案,即各种透视系统,可以分为概念系统和光学系统两大类。概念系统是按照一定的思路或原则来画人和物,与实际景物本身关系不大。例如,埃及绘画的浮雕作品大多遵循概念体系,人物的大小往往由他们在政治宗教阶层中的重要性决定。法老往往是最重要的人,所以他的体型最大,他的妻子比他小,他的仆人小得可怜。同一个人的不同部位,正面,侧面甚至同时。为了将一系列的人或动物成组地表现出来,采用的方法甚至是将同一幅图像的位置稍微缓慢地移动,使其重复出现。不仅是大部分的日本画和中国画,现代画(插图27)也是按照概念体系创作的。
在透视方面表现出杰出能力的画家是阿曼陀罗(1431-1506)。他把解剖和透视作为绘画的理想技巧。他选择疑难问题进行研究,用透视法实现自己严谨的求实作风和强烈的进取精神。在他的《圣詹姆斯导致处决》(图22)中,他故意选择了一个古怪的点。主消失点就在画的底部,在中心的右边。因为选择了这个不寻常的视点,整个画面处理的非常成功。

16世纪是伟大文艺复兴以来写实绘画发展的最高峰。这些作品表现了精准的透视和其表达的功能,注重空和色彩。完美的表达方式受到人们的喜爱,以至于艺术家对具体内容漠不关心。达芬奇的杰出学生米开朗基罗和拉斐尔创造了许多理想、标准和辉煌的成功范例,这些都是人们几个世纪以来梦寐以求的。拉斐尔的《雅典学派》(图23)描绘了一座布局和谐、透视巧妙、尺度清晰精确的神圣庄严的建筑。这幅画的意义不仅在于它巧妙地处理了空空间和景深,还在于它表达了文艺复兴时期有识之士对希腊先贤的崇敬。柏拉图和亚里士多德,一左一右,在画的中央。柏拉图左边是苏格拉底。在左边,毕达哥拉斯正在写一本书。在地面的右边,欧几里得或阿基米德蹲在那里证明定理。在图的右边,托勒美手里拿着一个球。全画有音乐家,数学家,语法学家。

16世纪著名的威尼斯画家在色彩、光影上附加了线条。但是,他们都掌握了透视法。空之间的表现完全是立体的,很明显画面是有组织的,用的是透视法。丁托列托(1518-1594)是这一画派的代表。他的《圣凯尔之体的转移》(插图24)非常恰当地处理了景深。前景中图像的前向收缩方法显然值得关注。我们再来看一个例子。

我们注意到,丢勒作为讨论透视的学者之一,对北阿尔卑斯山的画家产生了深远的影响。他的青铜雕塑“研究中的圣杰罗姆”(图25)展示了丢勒自己的透视法。画中的主要消失点位于画面的正中央,画面的效果让观者觉得他当时就在房间里,离圣杰罗姆只有几步之遥。

通过观察和推测威廉·霍加斯的题为“错误的视角”的铁板雕刻(图26),读者会发现其中许多是荒谬的,所以读者现在可以用视角来评估他们的知识水平。

像上面这样使用焦点透视系统的例子不胜枚举。但这些例子可以充分说明人们是如何用数学的视角将绘画从中世纪绘画的金色背景中解放出来,自由地描绘现实世界的街道、山川河流。这些例子也说明了聚焦透视法的第二个价值是画风的统一。我们所关注的这个体系的发展,也展示了一些合适的数学定理和以数学为基础的自然哲学,这有力地决定了西方绘画的进程。虽然现代绘画已经明显摆脱了对自然的直接描述,但艺术学校仍然教授对焦系统,并且在绘画中仍然广泛使用。在任何时候,透视系统对于实现真实的表达效果仍然非常重要。
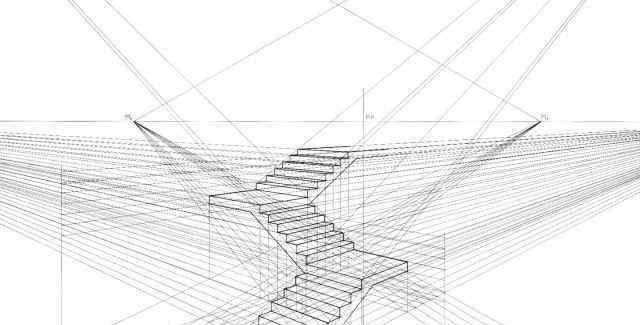
注:本文插图来自于Serena收集的wikiart。p并根据英文原著的插图进行编辑
关注我们
帮助孩子成长
给孩子最好的科学教育
1.《没影点 绘画与透视(西方文化中的数学)》援引自互联网,旨在传递更多网络信息知识,仅代表作者本人观点,与本网站无关,侵删请联系页脚下方联系方式。
2.《没影点 绘画与透视(西方文化中的数学)》仅供读者参考,本网站未对该内容进行证实,对其原创性、真实性、完整性、及时性不作任何保证。
3.文章转载时请保留本站内容来源地址,https://www.lu-xu.com/fangchan/876211.html





