在定量分析中,经常看到变量之间存在一定的关系。为了理解变量之间是如何相互作用的,我们需要使用相关分析和回归分析。在前一章中,对相关分析的相关内容进行了描述。本章介绍了回归分析的基本概念,回归分析的主要类型:一元线性回归分析、多元线性回归分析、非线性回归分析、曲线估计、时间序列的曲线估计、虚拟自变量回归分析和逻辑回归分析。
j .基本概念:
相关分析和回归分析是研究变量之间关系的统计学科。在应用中,两种分析方法往往相互结合、相互渗透,但研究重点和应用领域不同。在回归分析中,变量y被称为因变量,处于一个需要解释的特殊位置;在相关性分析中,变量y和变量x处于相等的位置,变量y和变量x的贴近度与变量x和变量y的贴近度相同。
回归分析中因变量Y是随机变量,自变量X可以是随机变量,也可以是非随机的确定性变量。在相关分析中,变量x和变量y都是随机变量。相关分析是衡量变量之间关系的紧密程度,使用的工具是相关系数;回归分析侧重于变量之间的数量变化规律,通过一定的数学表达式描述变量之间的关系,进而确定一个或几个变量的变化对另一个特定变量的影响程度。
具体来说,回归分析主要解决以下问题。
?通过分析大量样本数据,确定变量之间的数学关系。
?对确定的数学关系的可靠性进行各种统计检验,将对特定变量有显著影响的变量与无显著影响的变量区分开来。
?根据一个或几个变量的值,利用确定的数学关系来预测或控制另一个特定变量的值,并给出这种预测或控制的精度。
作为一种处理变量之间关系的统计方法和技巧,回归分析的基本思想和方法以及“回归”这个名称的由来都归功于英国统计学家F·高尔顿。
在实践中,根据变量的数量、变量的类型和变量之间的相关性,回归分析通常分为一元线性回归分析、多元线性回归分析、非线性回归分析、曲线估计、时间序列曲线估计、虚拟自变量回归分析和逻辑回归分析。
这种情况只能解释多元线性回归
在实际问题中,影响因变量的因素很多。
例如,对商品的需求不仅受自身价格的影响,还受消费者收入、其他商品价格、消费者偏好等因素的影响;影响果实产量的外部因素包括平均温度、平均日照时数、平均湿度等。
所以在很多场合,仅仅考虑单个变量是不够的,需要考察一个因变量和多个自变量之间的关系,才能得到满意的结果。这就导致了确定多个因素之间相关性的问题。
在线性相关条件下研究两个或两个以上自变量与一个因变量之间的定量关系,称为多元线性回归分析,表达这种定量关系的数学公式称为多元线性回归模型。多元线性回归模型是一元线性回归模型的扩展。其基本原理与一元线性回归模型相似,但计算较为复杂,一般需要计算机完成。



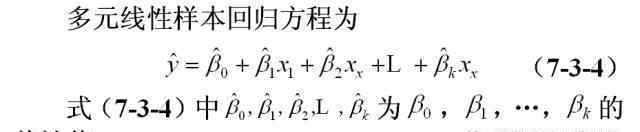



对于多元线性回归,还需要测量方程的拟合程度,检验回归方程和回归系数的显著性。
多元线性回归方程的显著性检验一般采用f检验和方差分析方法。
回归系数的显著性检验是检验各个变量x1,x2,…对因变量y是否有显著影响,从而找出哪些自变量对y有重要影响,哪些没有。
与线性回归一样,为了检验解释变量是否对因变量y有显著的线性影响,应使用t检验。
1.《多元回归 多元回归分析入门》援引自互联网,旨在传递更多网络信息知识,仅代表作者本人观点,与本网站无关,侵删请联系页脚下方联系方式。
2.《多元回归 多元回归分析入门》仅供读者参考,本网站未对该内容进行证实,对其原创性、真实性、完整性、及时性不作任何保证。
3.文章转载时请保留本站内容来源地址,https://www.lu-xu.com/guonei/1763860.html