空间统计：多距离空间聚类分析 (Ripley's K 函数)

转载自大虾卢博客

有种叫做“空间尺度”的概念，所以，在研究聚类的时候，最重要的就是确定不同数据之间的距离，否则就会如下：

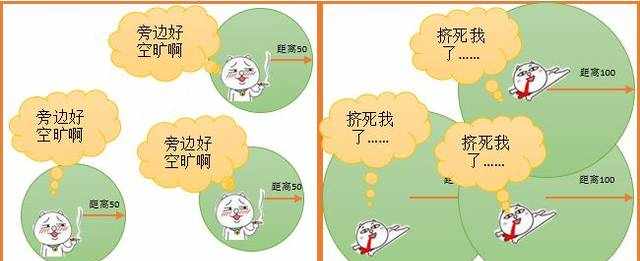
聚类分析中，要素之间的距离是个很重要的参数；也就是说两个要素相隔多远才算是聚成一类呢？在任何一种聚类算法中，探索一个合适的距离，都是比较纠结的事情。专家提出了各种算法，都想要优化这个距离探索的过程，以便有效的降低计算开销。

同样一份数据，在不同的距离上，表现出来的聚类效果肯定是不同的，所以我们今天来说一个灰常灰常神奇的工作，他不同于其他的分析工具的单一距离分析，他可以汇总在一定距离内所有数据的相关性进行汇总，以供我们选择适当的分析比例。

首先我们来看Ripley's K函数是个什么东西。Ripley's K方法是一种点数据模式的分析方法，它可以利用Ripley's K函数对点数据集进行不同距离的聚类程度分析，如下图所示：

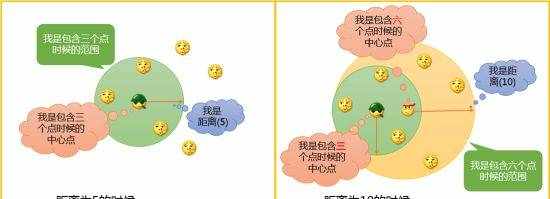
当距离为5的时候，要素的质心的位置和密度如左图所示，当距离扩大为10的时候，质心和包含的要素数量都会发生变化，那么数据的密度也会随之变化。

所以，Ripley's K函数就是用来表明这批要素的质心的空间聚集或空间扩散的程度，以及在邻域大小发生变化时是如何变化的。

我们来看看这个算法的基本原理。

首先我们要设定一个起算距离，当然，还可以指定最终距离或者增量步长，如开始为5，然后每次计算增加3这样的。计算的距离增加的时候，包含的相邻的要素自然就会原来越多，那么就可以针对不同的距离，去计算包含的数据的密度。

当全部算完之后，把每个距离的密度进行一下算数平均，并且用这个平均密度，作为用于比较的标准密度值。

然后用每个距离里面，包含的数据量的密度，来与标准密度值进行比较。大于标准密度，那么我们就认为这个距离上，数据处于聚类分布，而小于标准值的，我们就认为他处于离散分布。如下图所示：

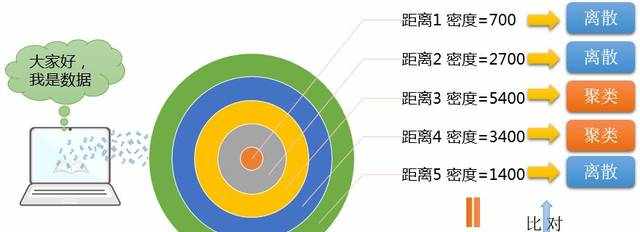
从上图可以看见，整个数据分布，其实不是线性，而这种所谓的离散或者距离，更多的是一种定性的说法，至于哪个距离上聚集效果好，哪个程度上离散程度大，一般是通过观察k值和预期k值进行比较得来的。

所谓的观察k值，指的是我们计算出来的实际密度值，而预期k值，指的是在随机分布的情况下，预期的分布情况。

有的同学就要问了，不是用的平均密度来进行比较么？这个预期K值和随机分布又是什么鬼？

平均值的问题，前面我们已经一而再再而三的说过了，虽然他简单好用，但是他的优点和缺点一样的明显，在描述算法的时候，可以用平均值来进行描述，但是实际使用中，平均值暴露出来的各种问题，会让分析人员为之抓狂。特别是在空间分布研究的时候。如果仅仅用平均密度来研究具有空间分析的数据，会出现如下问题：

所以为了避免平均数带来的一些简单粗暴的计算，在研究空间分布的时候，更多是利用零假设的方式，来设定随机数进行分布，作为预期值。

实际上，研究的方式是这样的：

在每个研究区域内，都进行随机假设，也就是独立的将每个研究预期中都采用零假设的方式设定期望值，这样的话就可以避免上面那种整体平均数出现的错误了。

所以，整个算法，在计算完成之后，会生成两个数据，一个叫做“观测K值”，一个叫做“期望K值”，他们的特点如下：

如果特定距离的 K 观测值大于 K 预期值，则与该距离（分析尺度）的随机分布相比，该分布的聚类程度更高。如果 K 观测值小于 K 预期值，则与该距离的随机分布相比，该分布的离散程度更高。

当然，任何的假设，最好需要设立一个置信度，进行验证的时候，首先就要决定我们来抛多少枚硬币，费希尔爵士也总结出了一个5%的规律。

当然，你也可以不设置置信度，这样的话，就表示怎么计算都行，只要得出结果就好了。

而效果比较好的，当然就是要设置一下执行度了。

在这个算法里面，确定期望K值时候，是要通过设立随机数来实现的，也就是说，你有100个数据，我就要生成100随机数，然后随机的分布在你的研究区域中，用这个随机分布的假设，来验证你的数据。

因为是随机数，所以放置这些随机数的时候，你也无法确定到底扔在那个地方，有可能都扔在一堆了……所以最好的方法，就是多设立几组随机数，多放置几次，以获得最佳效果。那么设立多少组随机数比较好呢？理论上来说，当然是越多越好，但是实际上不可能搞得非常多。在ArcGIS提供的多距离空间聚类分析 (Ripley's K 函数) 工具里面，给了“Compute_Confidence_Envelope”（计算置信区间）这样一个参数，一共给出了4个选项：

0_PERMUTATIONS_-_NO_CONFIDENCE_ENVELOPE —不创建置信区间。 9_PERMUTATIONS —随机放置了 9 组点/值。 99_PERMUTATIONS —随机放置了 99 组点/值。 999_PERMUTATIONS —随机放置了 999 组点/值。

其中：9 表示 90%，99 表示99%，999 表示 99.9%。

使用了这个参数之后，算法还会计算出LwConfEnv和 HiConfEnv这两个数据，他们分别表现每个迭代计算（由距离段数量参数指定）的置信区间信息。

如果观测K值大于 HiConfEnv 值，则该距离的空间聚类具有统计显著性。如果观测K值小于 LwConfEnv值，则该距离的空间离散具有统计显著性。

多距离空间聚类分析这个工具与其他的工具计算出来的结果都不太一样。按照空间分析软件的一般规律，扔进去的是一个空间数据，那么返回的自然也是一个空间数据……

不过在前面也很多分析工具告诉我们，可能就会返回几个数据给你，比如莫兰指数，给你几个值来表示一下。这个多距离空间聚类分析工具为为什么会让我们觉得神奇呢？因为他的返回值很神奇——它会返回一堆的数字给你。

返回的值以及含义如下：

说明图：

一般根据你设定的距离，会返回一堆的数据，如：

把这些数据整体画出来，就会变成这个样子

无论是从表信息里面，还是从图上，我们都可以看见，当第五次计算的时候，也就是预期K值（预期K值一般等于距离）等于33517的时候，观测K与预期K值的差距最大，聚类程度最高。

因为这个工具的交互能力比较强，也就是说，设定不同的参数，返回的内容差很多，所以今天得破例讲讲工具的各种使用参数，如下：

整个工具有11个参数，但是实际上除去默认的几个参数以外，你只需要填入两个参数就行，一个是输入的要用于计算的要素图层，一个就是输出的表格了。

下面把以下参数解释一下，简单的我就略过了。

先说说距离的选择相关的三个参数，分别是

Number_of_Distance_Bands 距离的变化次数（递增次数） Beginning_Distance （起算距离） Distance_Increment （递增步长）

这三个参数理论上一起用的，只不过距离的的变化次数默认就直接给你是10次，而起算距离和递增步长作为可选参数。

起算距离参数如果你不指定的话，系统会设定一个默认值。默认值是设定你的最大范围，在ArcGIS里面，这个默认最大距离就是整个数据范围的25%。而如果有了起算距离，那么距离增量=（最大距离 - 开始距离）/迭代值

然后我们来看看权重这个东西。

其实权重在空间计算里面，一直是个很重要的东西，还是引用毛博士语录：凡事不考虑属性的空间聚类，都是耍流氓……所以在空间分析里面，很多时候属性被体现在权重上面。

第三来看看随机模拟的次数，这个表示我们给出多少组模拟数据，来设定置信度的问题，如果你选择“0_PERMUTATIONS_-_NO_CONFIDENCE_ENVELOPE”这个参数，也就表示不创建置信区间。那么你的结果里面，就不会出现LwConfEnv和HiConfEnv这两个数据了。

那选择其他三个参数，如下：

9_PERMUTATIONS —随机放置了 9 组点/值。 99_PERMUTATIONS —随机放置了 99 组点/值。 999_PERMUTATIONS —随机放置了 999 组点/值。

其中：9表示 90%，99 表示 99%，999 表示 99.9%。

因为K函数有一个特点，就是对位于研究区域边界附近的要素具有统计缺漏偏差（也叫不完全统计偏差：undercount bias ，也就电视里面经常说的“据不完全统计”……指不能完全预见统计内可能出现的各种情况，从而无法达成内容完备、设计周详的统计。）。

所以上面提供边界校正方法参数提供了解决这一偏差的方法。（查看参数说明中的第9个参数）

·NONE

如果应用这种参数，表示不应用任何特定的边界校正。但是，落在用户指定的研究区域外的点在相邻点计数中使用。如果我们的数据是从超大研究区域中收集数据，但是仅需分析数据集合边界内更小的区域，则此方法很适用。如下图：

·SIMULATE_OUTER_BOUNDARY_VALUES

此方法会在研究区域边界外，创建边界内所发现点的镜像点，以便校正边附近的低估现象。将镜像与研究区域的边的最大距离范围相等的距离内的点。使用已镜像的点会使边点的相邻点估计更加精确。下图说明哪些点用于计算以及哪些点仅用于边校正。

·REDUCE_ANALYSIS_AREA

此边校正技术将分析区域的大小收缩一定的距离，此距离与将在分析中使用的最大距离范围相等。收缩研究区域后，仅在为仍处于研究区域内的点评估相邻点数目时，才会考虑新研究区域外发现的点。K 函数计算期间，不会以任何其他方式使用这些点。下图说明哪些点用于计算以及哪些点仅用于边校正。

RIPLEY'S_EDGE_CORRECTION_FORMULA

此方法检查每个点与研究区域的边的距离以及这个点到其各相邻点的距离。如果有的相邻点与所涉及点的距离比与研究区域的边的距离更远，则所有这类相邻点都将被指定额外权重。此边校正方法仅适用于形状为正方形或矩形的研究区域，或者当为研究区域方法参数选择 MINIMUM_ENCLOSING_RECTANGLE 时才适用。

这个方法有人会问，这么复杂的方法，如此多的参数，他到底想解决的是什么问题呢？这个主要解决的边界点邻近的问题，如下图所示：

最后来看看参数10，也就是研究区域的问题。这个问题在经典统计学里面，是个很重要的问题，特别是对于K函数这种对距离很敏感的方法，那么它提供了两种限定研究区域的方法，如下：

·MINIMUM_ENCLOSING_RECTANGLE —指示将使用封闭所有点的最小矩形。如下图：

·USER_PROVIDED_STUDY_AREA_FEATURE_CLASS —指示定义研究区域的要素类将在“研究区域要素类”参数中提供。

OK，到此，所有的输入参数都说完了，最后用几句话，来说说这个方法到底有什么作用。

在上一篇文章中，其实已经讲过，距离的探索是点模式分析中很重要的一个工作，实际他的应用非常的多，如下面的几种应用：

城市里面有若干巡逻热点，如果警方要部署巡逻区域，怎么才能找到即省油，又能尽量的覆盖到所有的巡逻热点这样的分析中，就可以采用距离分析，探索每个设定的巡逻区域的最佳距离。

另外，我有一批点，我现在要用这些点生成一个缓冲区，这个缓冲区需要覆盖所有的区域，但是又要求缓冲区的距离是最小的，那么就可以通过这个工具，来找到聚类程度最高的一个距离，如下：

对照一下图，我们可以看出，聚类程度最高的数据，用于计算这类缓冲区，效果是最好的。实际数据统计图如下：