题目:
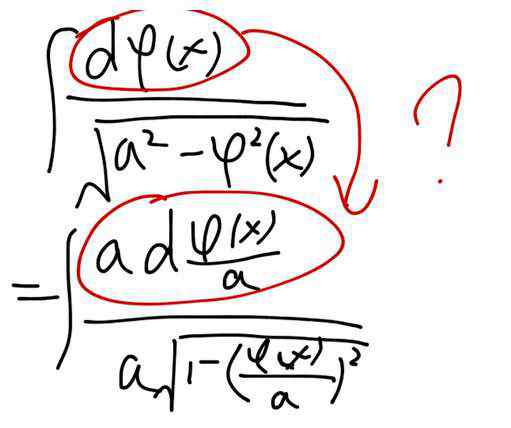
分布积分具体操作如:根据“反对幂三指”先后顺序,前者为u,后者为v(例:被积函数由幂函数和三角函数组成则按口诀先积三角函数(即:按公式∫udv = uv - ∫vdu + c把幂函数看成U,三角函数看成V,)).原公式:(uv)"=u"v+uv"求导公式 :d(uv)/dx = (du/dx)v + u(dv/dx) 写成全微分形式就成为 :d(uv) = vdu + udv移项后,成为:udv = d(uv) -vdu两边积分得到:∫udv = uv - ∫vdu在传统的微积分教材里分部积分法通常写成不定积分形式:∫v(x)u"(x)dx=v(x)u(x)- ∫v"(x)u(x)dx请问为什么可以写成∫v(x)u"(x)dx=v(x)u(x)- ∫v"(x)u(x)dx,写成这样有什么用
解答:

名师点评:
怪叔叔疾m5琞
1.《反对幂指三 分布积分具体操作如:根据“反对幂三指”先后顺序,前者为u,后者为v(例:被积函数由幂函数和三角函数组成则按口诀先积三角函》援引自互联网,旨在传递更多网络信息知识,仅代表作者本人观点,与本网站无关,侵删请联系页脚下方联系方式。
2.《反对幂指三 分布积分具体操作如:根据“反对幂三指”先后顺序,前者为u,后者为v(例:被积函数由幂函数和三角函数组成则按口诀先积三角函》仅供读者参考,本网站未对该内容进行证实,对其原创性、真实性、完整性、及时性不作任何保证。
3.文章转载时请保留本站内容来源地址,https://www.lu-xu.com/jiaoyu/428622.html