向量内积的运算：(x·y)=(y·x)；(x+y)·z=(x·z)+(y·z)；(kx·y)=k(x·y)；(x·x)=x1^2+......+xn^2>=0等号成立当且仅当x=0。
运算法则
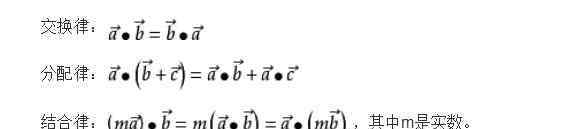
1.《向量内积 向量内积怎么算》援引自互联网，旨在传递更多网络信息知识，仅代表作者本人观点，与本网站无关，侵删请联系页脚下方联系方式。
2.《向量内积 向量内积怎么算》仅供读者参考，本网站未对该内容进行证实，对其原创性、真实性、完整性、及时性不作任何保证。
3.文章转载时请保留本站内容来源地址，https://www.lu-xu.com/jiaoyu/446875.html
已知直线l：ax+by+c=0，则直线l的方向向量为s=(-b，a)或(b，-a)；若直线l的斜率为k，则l的一个方向向量为s=(1，k)；若A(x1，y1)，B(x2，y2)，则AB所在直线的一个方向向量为s=(x2-x1，y2-y1)。方向向量的求解只要给定直线，便可构造两个方向向量（以原点为起点）。（1）即已知直线l：ax+by+c=0，则...
平面向量的坐标运算：AB+BC=AC；AB-AC=CB；(λμ)a=λ(μa)；(λ+μ)a= λa+μa；a·a=|a|²；a·b=b·a等。坐标运算向量的数量积的性质(1)a·a=∣a∣²≥0(2)a·b=b·a(3)k(ab)=(ka)b=a(kb)(4)a·(b+c)=a·b+a·c(5)a·b=0a⊥b(6)a=kba//b(7)e1·...
积分的运算法则：积分的运算法则，别称积分的性质。积分是线性的。如果一个函数f可积，那么它乘以一个常数后仍然可积。如果函数f和g可积，那么它们的和与差也可积。通常意义积分都满足一些基本的性质。以下的I在黎曼积分意义上表示一个区间，在勒贝格积分意义下表示一个可测集合。线性积分是线性的。如果一个函数f可积，那么它乘以一个常数后仍然可积。如果函数f和g可...
空间直线点向式方程的形式为（和对称式相同）：(x-x0)/l=(y-y0)/m=(z-z0)/n，其方向向量就是（l，m，n）或反向量（-l，-m，-n）。空间直线的一般方程求方向向量空间直线点向式方程的形式为（和对称式相同）(x-x0)/l=(y-y0)/m=(z-z0)/n，其方向向量就是（l，m，n）或反向量（-l，-m，-n）。比如直线x...
指数的运算法则：同底数幂的乘法：底数不变，指数相加幂的乘方；同底数幂的除法：底数不变，指数相减幂的乘方。指数的运算法则指数运算法则口诀同底数幂的乘法：底数不变，指数相加幂的乘方；同底数幂的除法：底数不变，指数相减幂的乘方；幂的指数乘方：等于各因数分别乘方的积商的乘方分式乘方：分子分母分别乘方，指数不变。指数函数指数函数的一般形式为y=a^x(a>...
指数的运算法则：同底数幂的乘法：底数不变，指数相加幂的乘方；同底数幂的除法：底数不变，指数相减幂的乘方。指数的运算法则指数运算法则口诀同底数幂的乘法：底数不变，指数相加幂的乘方；同底数幂的除法：底数不变，指数相减幂的乘方；幂的指数乘方：等于各因数分别乘方的积商的乘方分式乘方：分子分母分别乘方，指数不变。指数函数指数函数的一般形式为y=a^x(a>...
指数的运算法则：同底数幂的乘法：底数不变，指数相加幂的乘方；同底数幂的除法：底数不变，指数相减幂的乘方。指数的运算法则指数运算法则口诀同底数幂的乘法：底数不变，指数相加幂的乘方；同底数幂的除法：底数不变，指数相减幂的乘方；幂的指数乘方：等于各因数分别乘方的积商的乘方分式乘方：分子分母分别乘方，指数不变。指数函数指数函数的一般形式为y=a^x(a>...
