stacking 深度 | 从Boosting到Stacking，概览集成学习的方法与性能

选自Statsbot

参与:简w。

集成学习通过结合几种模型来提高机器学习的效果。与单一模型相比，该方法能提供更好的预测结果。正因为如此，这种集成方法可以在许多著名的机器学习比赛(如网飞、KDD 2009和卡格尔比赛)中获得良好的排名。

集成方法是一种将几种机器学习技术结合到预测模型中的元算法，以达到减少方差(打包)、提高或改善预测(堆叠)的效果。

设置方法可以分为两类:

序列整合法，其中参与训练的基础学习者按顺序生成(如AdaBoost)。序列法的原理是利用基础学习者之间的依存关系。通过在先前的训练中给错误标记的样本分配更高的权重，可以提高整体预测效果。

并行集成法，参与训练的基础学习者并行生成(如Random Forest)。平行法的原理是利用基础学习者之间的独立性，通过平均显著减少错误。

大多数整合方法使用单一的基本学习算法来产生同构的基本学习者，即同类型的学习者，这就是同构整合。

也有一些方法使用异构学习者，即不同类型的学习者，这是异构整合。为了使积分方法比任何单一算法更精确，基础学习者必须尽可能精确和多样。

装袋

打包是引导聚合的缩写。降低估计方差的一种方法是将多个估计值一起平均。例如，我们可以在不同的数据子集上训练m个不同的树(随机选择)，并计算集成结果:

Bagging使用bootstrap采样来获得用于训练基础学习者的数据子集。Bagging使用投票分类和均值回归来聚合基础学习者的输出。

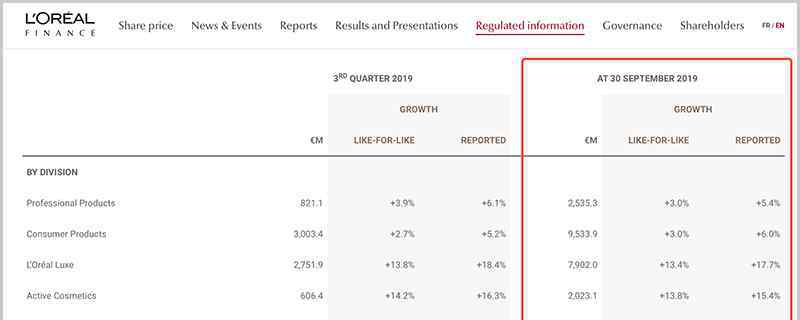
我们可以研究bagging方法对虹膜数据集的分类效果。为了比较预测结果，我们选择了两个基准估计量:决策树和k-NN分类器。图1显示了基准估计器和bagging集成算法在Iris数据集上的学习决策边界。

准确度:0.63(+/- 0.02)[决策树]

精度:0.70(+/- 0.02)[K-NN]

准确度:0.64(+/-0.01)[装袋树]

准确度:0.59(+/-0.07)[装袋K-NN]

决策树的判决边界与轴平行，而K-NN算法的判决边界在k=1时靠近数据点。Bagging集成了10个用于训练的基本估计量，其中训练数据的采样概率为0.8，特征的采样概率为0.8。

与k-NN装袋集成相比，决策树装袋集成具有更高的准确率。K-NN对训练样本的扰动不太敏感，因此被称为稳定学习器。

综合稳定学习者不利于提高预测效果，因为综合方法无助于提高泛化性能。

最右边的图还显示了测试集的准确性如何随着集成的大小而增加。根据交叉验证的结果可以看出，精度随着估计量的增加而增加，当基本估计量约为10个时达到最大，然后保持不变。因此，对于Iris数据集，增加10个以上的基本估计量只是增加了计算复杂度，并没有增加精度。

我们也可以看到装袋树集成的学习曲线。注意训练数据的平均误差为0.3，测试数据为U型误差曲线。训练误差和测试误差之间的最小差异出现在训练集大小的大约80%。

一种常见的集成算法是随机森林。

在随机森林中，集合中的每棵树都是由从训练集中提取的样本(引导样本)构建的。另外，不同于使用所有特征，这里随机选取特征子集，进一步达到随机化树的目的。

因此，随机森林造成的偏差略有增加，但通过计算相关性较小的树的平均值来降低估计方差，从而导致模型的整体效果更好。

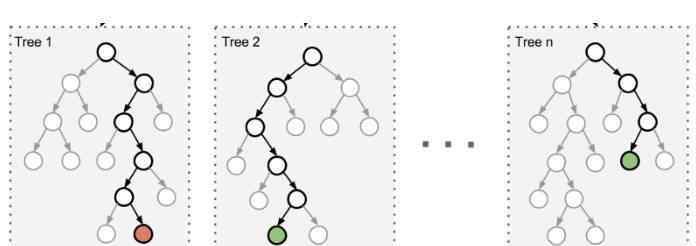
在极随机化树算法中，随机性进一步增加:分割阈值是随机的。不同于寻找区分度最高的阈值，每个候选特征的阈值都是随机选取的，这些随机产生的阈值的最佳值将作为分割规则。这通常会降低模型的方差，但代价是偏差略有增加。

提高

Boosting是一类可以将弱学习者转化为强学习者的算法。Boosting的主要原理是适应一系列弱学习者模型，只比随机猜测稍微好一点，比如小决策树-数据加权模型。重量分配早期训练中错误分类的更多例子。

然后，通过组合加权多数投票(分类)或加权求和(回归)来生成最终预测。Boosting和bagging的主要区别在于基础学习者通过加权数据进行顺序训练。

下面的算法说明了最广泛使用的boosting算法，称为AdaBoost，是自适应boosting的缩写。

我们看到第一个基本分类器y1(x)使用所有相等的权重进行训练。在随后的提升训练中，错误分类的数据点的系数权重增加，而正确分类的数据点的系数权重减少。

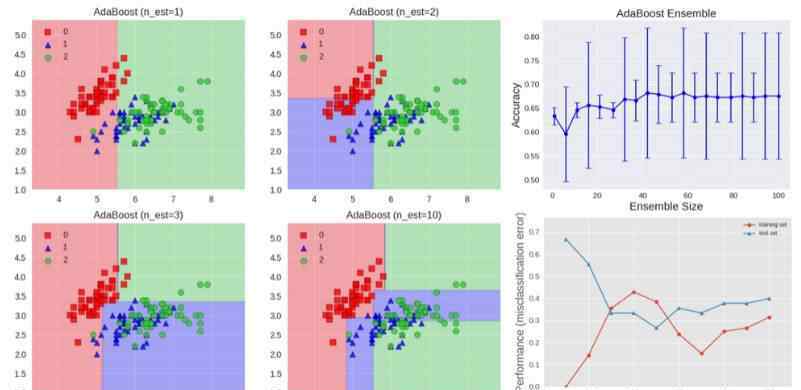
ε值代表每个基本分类器的加权误差率。因此，系数权重α为更精确的分类器分配更大的权重。

AdaBoost算法如上图所示。每个基本学习者由深度为1的决策树组成，决策树根据特征阈值对数据进行分类，特征阈值将空划分为两个区域，两个区域由平行于一个轴的线性决策面分隔开。图中还显示了测试集的准确性随着集大小的增加而提高，并显示了训练数据和测试数据的学习曲线。

梯度树增强是使用任何可微分损失函数的增强的推广。它可以用于回归和分类问题。梯度增强以连续的方式构建模型。

在每一步，给定当前模型Fm-1(x)，决策树hm(x)通过最小化损失函数l来更新模型:

回归和分类算法在所使用的损失函数类型上是不同的。

堆

堆叠是一种集成的学习技术，它通过元分类器或元回归聚集多个分类或回归模型。基于完整的训练集训练层次模型，然后基于层次模型的输出训练元模型。

基本层通常由不同的学习算法组成，因此堆叠集成通常是异构的。以下算法总结了堆叠算法的逻辑:

以下是几种算法的准确率，如上图右侧的图表所示:

精度:0.91(+/- 0.01)[K-NN]

精度:0.91(+/- 0.06)[随机森林]

准确度:0.92(+/- 0.03)[朴素贝叶斯]

精确度:0.95(+/-0.03)[堆叠分类器]

堆叠集成如上图所示。它由k-NN、随机森林和朴素贝叶斯分类器组成，其预测结果通过逻辑回归组合成元分类器。我们可以看到堆叠分类器实现的混合决策边界。该图还表明，叠加可以获得比单个分类器更高的精度，并且从学习曲线来看，它没有显示出过度拟合的迹象。

在Kaggle数据科学竞赛中，堆叠等技术往往会赢得比赛。比如在奥托集团产品分类挑战赛中获得第一名所使用的技术就是堆叠，它集成了30多个模型，其输出是3个元分类器的特征:XGBoost、神经网络和Adaboost。详见以下链接:https://www . kaggle . com/c/Otto-group-product-classification-challenge/discussion/14335。

代码

有关生成文本中所有图片的代码，请参见ipython笔记本:

https://github . com/vsmolyakov/experiments _ with _ python/blob/master/chp 01/ensemble _ methods . ipynb .

结论

除了本文研究的方法之外，深度学习通常通过训练多样且准确的分类器来使用综合学习方法。其中，多样性可以通过改变体系结构、超参数设置和训练技术来实现。

集成学习非常成功。该算法不仅在具有挑战性的数据集上频繁打破性能记录，而且是卡格尔数据科学竞赛获胜者常用的方法之一。

原地址:https://blog.statsbot.co/ensemble-learning-d1dcd548e936

这篇文章是为机器的核心编写的。请联系该公众号进行授权。