一次函数试题八年级数学，一次函数专题复习训练题附及答案

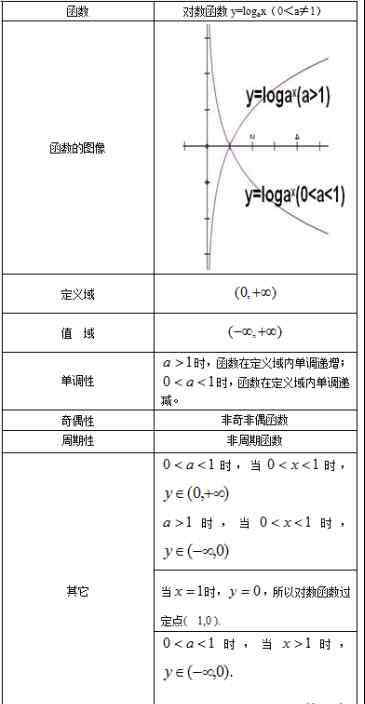
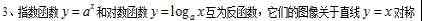1.如果比例函数为y = 3x的图像通过点(1，m)，则m的值为()

A.B.3 C.- D.-3

2.让比例函数y = MX的图像通过点A(m，4)，y的值随着x值的增大而减小，然后m =()

A.2 B.-2 C.4 D.-4

在平面直角坐标系中，如果直线y = kx+b通过第一、第三和第四象限，则直线y = bx+k不通过的象限为()

A.第一象限第二象限第三象限第四象限

4.关于直线l: y = kx+k (k ≠ 0)，以下说法不正确()

A.点(0，k)在l b上。l通过固定点(-1，0)

C.当k >: 0时，y随着x的增加而增加，d.l穿过第一、第二和第三象限

5.比例函数y = kx的图像如图所示，那么k的取值范围是()

A.k>。0 B.k & lt0°c . k >；1d . k & lt；一个

6.如果函数y = kx-b的像如图所示，则关于x的不等式k (x-3)-b > 0的解集为()

主要功能主题复习培训问答

6个问题

A.x<2 B.x>2 C.x<5 D.x>5

7.在平面直角坐标系中，通过点(-2，3)的直线L经过第一、第二、第三象限。如果点(0，a)，(-1，b)，(c，-1)都在直线L上，那么下面的判断是正确的()

a . a < b . b . a < 3c . b < 3d . c <-2

8.在同一直角坐标系中，线性函数Y1 = K1x+B和比例函数Y2 = K2x的图像如图所示，则满足y1≥y2的X的取值范围为()

主要功能主题复习培训问答

九个问题

A.x=2 B.x=0 C.x=-1 D.x=-3

10.在平面直角坐标系中，平移直线L1: y =-2x-2后，得到直线L2: y =-2x+4，则下面的平移方法是正确的()

A.将l1向右平移3个单位长度

C.将l1向上平移2个单位长度

11.对于函数y =-3x+1，以下结论是正确的()

A.它的图像必须通过点(-1，3)

B.其图像穿过第一、第二和第三象限

C.当x > 1时，y < 0

d.y值随着x值的增加而增加

12.如果直线y = kx+3通过点a (2，1)，则不等式kx+3 ≥ 0的解集为()

a . x≤3 b . x≥3 c . x≥3d . x≤0

13.如果初等函数y = kx+b (k，b是常数，k≠0)的图像通过第一、第二和第四象限，那么k和b应该满足的条件是()

A.k > 0，b > 0，b. k < 0，b > 0

C.k > 0，b < 0 d. k < 0，b < 0

14.如果已知点(-1，y1)，(4，y2)在线性函数y = 3x-2的图像上，那么y1，y2和0的大小关系是()

a . 0 < y1 < y2 b . y1 < 0 < y2 c . y1 < y2 < 0d . y2 < 0 < y1

15.如图所示，通过点a的线性函数的图像和比例函数y = 2x的图像在点b相交，则该线性函数的解析表达式为()

主要功能主题复习培训问答

15个问题

a . y = 2x+3 b . y = x-3 c . y = 2x-3d . y =-x+3

16.在平面直角坐标系中，已知初等函数y = 2x+1的图像穿过P1(x1，y1)和P2(x2，y2)。如果x1 < x2，则y1 _ _ _ _ y2。(填写">"，"

17.如果主函数y = kx+b (k ≠ 0)的图像通过点a (1，0)和b (0，2)，则它的图像不通过象限。

18.如果比例函数y = kx的图像通过点(1，2)，k = _ _。

19.将直线y =-x-1沿x轴向右平移2个单位，直线的分辨率函数为。

20.主函数y = kx+b (k，b为常数，k≠0)的图像如图所示。根据图像信息，可以如下获得关于x的方程kx+b = 0的解。

主要功能主题复习培训问答

20个问题

21.在平面直角坐标系中，已知点a (2，3)，b (4，7)，直线y = kx-k (k ≠ 0)与线段AB有交点，所以k的取值范围为。

22.在平面直角坐标系xOy中，点a和b的坐标分别为(3，m)和(3，m+2)，直线y = 2x+b与线段AB有一个公共点，所以b的取值范围为(用含有m的代数表达式表示)。

23.已知直线L1: y = x+n-2和直线L2: y = MX+n在点p (1，2)相交。

(1)求m和n的值；

(2)请直接用图像写出不等式MX+n > x+n-2的解集。

主要功能主题复习培训问答

23个问题

24.已知线性函数y = 2x-4的图像分别在点a和b处与x轴和y轴相交，点p在该函数的图像上，p到x轴和y轴的距离分别为d1和d2。

(1)当p为线段AB的中点时，求D1+D2的值；

②直接写出D1+D2的范围，求出D1+D2 = 3时p的坐标；

③如果线段AB上有无数个p点，设D1+ad2 = 4 (a为常数)求a的值.

主要功能主题复习培训问答

24个问题

25.一所学校组织275名师生在青年活动中心参加劳动技术活动。拟租甲、乙类公交车7辆，已知甲类公交车载客30人，乙类公交车载客45人。其中，每辆B类公交车的租金比A类公交车多100元，5辆A类公交车和2辆B类公交车的总租金为2300元。

(1)租一辆A类车和一辆B类车多少钱？

(2)出租甲类X客车，总租赁费W元。求W和X的函数关系；

在保证全部275名师生都有座位的前提下，租用一辆A类公交车时，租赁总成本最小，计算成本最小。

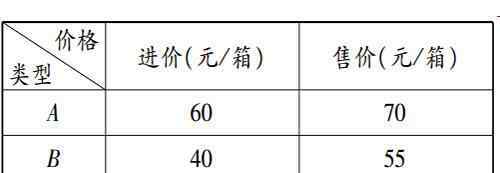
26.一家水果公司计划购买200盒A和B水果。这两种水果的收购价格和销售价格如下表所示:

主要功能主题复习培训问答

26个问题

(1)如果商号的购买价格为1万元，购买多少箱两种水果？

(2)如果事务所规定A水果的箱数不小于B水果的箱数，那么该事务所如何在这批水果销售一空后获得最大利润？这个时候的利润是多少？

27.某蔬菜加工公司分两批采购了100吨蒜薹。第一批蒜梗价格4000元/吨；由于市场上大量的蒜薹，第二批价格降至1000元/吨。两批蒜薹共16万元。

(1)蒜苗分两批采购多少吨？

(2)公司收购后，蒜薹加工，分为粗加工和精加工。粗加工每吨利润400元，精加工每吨利润1000元。要求精加工的数量不超过粗加工的三倍。为了获得最大利润，精加工的数量应该是多少吨？最大利润是多少？

参考答案:

1 - 15支BBCDA

16.<

17.三

18.2

19.y=-x+1

20.x=-1

21.≤k≤3

22.m-6≤b≤m-4

23.解:(1)将p (1，2)代入y = x+n-2得到1+n-2 = 2，解n = 3；

将P (1，2)代入Y = MX+3得到M+3 = 2，求解M =-1；

(2)不等式MX+n > x+n-2的解集为x < 1。

24.解:①对于一阶函数y = 2x-4设x = 0，得到y =-4；设y = 0，得到x = 2，∴ a (2，0)，B(0，-4)，* p是AB的中点，∴P(1,-2)，那么D1+D2 = 3；

②(ⅰ)D1+D2≥2；(ⅱ)设P(m，2m-4)，∴ D1+D2 = | m |+| 2m-4 |，当0≤m≤2，D1+D2 = m+4-2m = 4-m = 3时，解为:m = 1，则P1(m > 2时为1，D1+D2 = m+2m-4 = 3，解为:m =，则P2(，；当m < 0时，不存在。综上，p的坐标是(1，-2)或(，)；

③设P(m，2m-4)，∴ D1 = | 2m-4 |，D2 = | m |,∫p在AB线上，∴0≤m≤2，∴ D1 = 4-2m，D2 = m，∫D1+。

26个问题的答案如下: