第三次数学危机 数学历史上的三次危机

无理数的发现——第一次数学危机

大约在公元前5世纪，不可通约性的发现导致了毕达哥拉斯悖论。当时的毕达哥拉斯学派非常重视对自然界和社会中不变因素的研究，把几何、算术、天文、音乐称为“四大艺术”，在其中追求宇宙的和谐规律性。他们认为宇宙中的一切都可以归结为整数或整数之比，毕达哥拉斯学派证明了毕达哥拉斯定理，但也发现有些直角三角形的斜边不能表示为整数或整数之比(不可公度性)，比如直角都是1的直角三角形。这种悖论直接违背了毕学派的根本信条，导致了当时认知的“危机”，从而导致了第一次数学危机。

公元前370年，比西学派的欧多克索斯通过给比例一个新的定义解决了这个矛盾。他处理不可公度量的方法出现在欧几里得的《元素》第五卷。欧多克索斯和戴德金德1872年对无理数的解释与现代解释基本一致。中学几何教材中对相似三角形的处理仍然反映出不可通约性带来的一些困难和微妙之处。第一次数学危机对古希腊的数学观点产生了巨大的影响。这说明几何的一些真理与算术无关，几何量不能完全用整数及其比值来表示，而是可以用几何量来表示。整数的权威地位开始动摇，而几何的同一性上升。危机也说明，直觉和经验不一定可靠，但推理证明是可靠的。从此，希腊人开始重视解释和推理，从而建立了几何公理体系，这是数学思想的一次伟大革命！

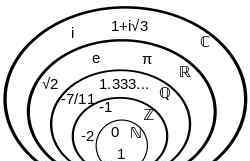
无穷大是零吗？第二次数学危机

18世纪，微分法和积分法在生产和实践中得到了广泛而成功的应用，大多数数学家对这一理论的可靠性毫不怀疑。

1734年，英国哲学家兼大主教贝克勒出版了《一个不相信正统的数学家的分析师或降临节》，指出微积分的基础——无穷小问题，提出了所谓的贝克勒悖论。他指出:“牛顿在求xn的导数时，首先给X一个0的增量，应用二项式(x+0)n，从中减去xn得到增量，再除以0得到xn的增量与X的增量之比，然后让0消失，从而得到最终的增量比。这里牛顿已经办理了违反矛盾律的手续——假设X有增量，增量为零，即假设X没有增量。”他认为无穷小dx既等于零又不等于零，被人叫着挥之不去是荒谬的。“dx是失去数量的灵魂”。无穷小到底是不是零？无穷小及其分析是否合理？这在数学乃至哲学领域引起了一个半世纪的争议。导致了数学史上的第二次数学危机。

18世纪的数学思想真的不严谨，不顾基础的可靠性，直观地强调形式计算。特别是没有明确的无穷小概念，所以导数、微分、积分的概念不清，无穷的概念不清，发散级数求和的任意性，符号的使用不严格，微分不考虑连续性，不考虑导数和积分的存在，函数是否可以展开成幂级数。

直到19世纪20年代，一些数学家更加注重微积分的严格基础。从波尔扎诺、阿贝尔、柯西、德赖克利等人的工作到威勒斯特拉斯、戴德金、康托尔的工作结束，历时半个多世纪，基本解决了矛盾，为数学分析奠定了严密的基础。

悖论的出现——第三次数学危机

数学史上的第三次危机产生于1897年的突然冲击。到目前为止，总体上还没有解决到满意的程度。这场危机是由康托尔的一般集合论边缘发现的悖论引起的。由于集合的概念已经渗透到数学的许多分支，事实上集合论已经成为数学的基础，集合论中悖论的发现自然引起了对数学整个基本结构有效性的怀疑。

1897年，福尔蒂揭示了集合论中的第一个悖论。两年后，康托尔发现了一个非常相似的悖论。1902年，罗素发现了另一个悖论，这个悖论除了集合本身的概念之外，不涉及其他概念。罗素悖论以多种形式得到了推广。最著名的是罗素在1919年发表的一篇文章，其中涉及到一个村庄理发师的困境。理发师宣布了这样一个原则:他给每个不刮胡子的人刮胡子，只刮村里的人。当人们试图回答以下问题时，他们意识到这种情况的矛盾性:“理发师自己刮胡子吗？”如果他不刮胡子，那么他就应该按照原则刮胡子；如果他自己刮胡子，那他就不符合他的原则。

罗素悖论动摇了整个数学大厦。难怪弗雷格在收到罗素的信后，在即将出版的《算术基本定律》第二卷末尾写道:“一个科学家，不可能遇到比这更尴尬的事了，那就是当工作完成时，它的基础崩塌了，当这本书等待印刷时，罗素先生的一封信把我置于这种境地”。就这样结束了将近12年的辛苦。

承认无限集合，承认无限基数，仿佛一切灾难都已经出来了，这就是第三次数学危机的本质。虽然悖论可以消除，矛盾可以解决，但数学的确定性是一步步丧失的。现代公理集合论中的很多公理很难说是真是假，但也无法排除。它们与整个数学密切相关。所以第三次危机表面上解决了，实质上是以其他形式继续。

用计算的力量改变世界是每个程序员的梦想，yak正在用计算把教育和科学变成生活的财富。融合艺术、算法、数学完成全新的表达，借助计算模拟重新学习物理化学，从数据的角度重新审视社会科学。从这些角度来看，牦牛可以成为一个启示，帮助儿童启蒙，帮助每个未来的数字公民真正理解现代科技的剧变带来的生产力的巨大解放，真正适应未来社会的不确定性。