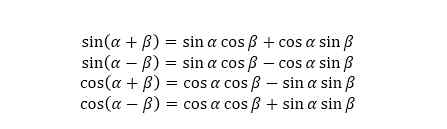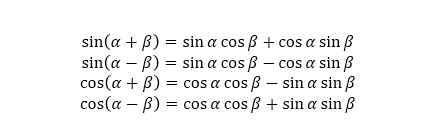二次函数性质 初中数学：一次/二次函数性质必考总结

线性函数

一.定义和定义:

自变量x与因变量y的关系如下:y = kx+b；这时，y被称为X的线性函数..

特别地，当b=0时，y是X的比例函数..即y=kx (k为常数，k≠0)

第二，第一个功能的性质:

1.y的变化值与x的变化值成正比，比值为k；即y=kx+b (k为任意不为零的实数，b为任意实数)

2.当x=0时，b是函数在y轴上的截距。

第三，一阶函数的图像和性质:

1.方法和图形:通过以下三个步骤

2.性质:(1)线性函数上的任意点P(x，Y)满足方程:Y = kx+b(2)初等函数与Y轴的交点坐标始终为(0，b)，以(-b/k，0)的比例函数始终与X轴相交的像始终与原点相交。

3.函数图像的k、B和象限:

当k > 0时，直线必须经过第一、三象限，y随着x的增大而增大；

当k < 0时，直线必须经过第二、四象限，y随着x的增大而减小。

当b > 0时，直线必须经过第一象限和第二象限；

当b=0时，直线穿过原点

当b < 0时，直线必须经过三四个象限。

特别地，当b=O时，直线表示通过原点o (0，0)的比例函数的图像。

此时，当k > 0时，直线只经过第一、三象限；当k < 0时，直线只经过第二、四象限。

第四，确定主函数的表达式:

已知点A(x1，y1)；B(x2，y2)，请确定通过a点和b点的线性函数的表达式。

二次函数

首先，定义和定义表达式

一般自变量x和因变量y有如下关系:y = ax ^ 2+bx+c；(a，b，c为常数，a≠0，a决定函数的打开方向，a >: 0，打开方向向上，a

y叫x的二次函数，二次函数表达式的右边通常是二次三项式。

二次函数和二次函数的三种表达式

通式:y = ax ^ 2+bx+c(a，b，c为常数，a≠0)

顶点:y = a(x-h)2+k[抛物线P(h，k)的顶点]

交点:y = a(x-x1)(x-x2)[只有a (x1，0)和b (x2，0)与x轴相交的抛物线]

注:相互变换的三种形式中，有以下关系:h =-b/2ak =(4ac-b ^ 2)/4ax？，x？=(-b √b^2-4ac)/2a

三次和二次函数的图像

在平面直角坐标系中作二次函数y = x 2的像，可以看出二次函数的像是抛物线。

第四，抛物线的性质

1.抛物线是轴对称图形。对称轴为直线x= -b/2a。

对称轴与抛物线唯一的交点是抛物线的顶点p。特别地，当b=0时，抛物线的对称轴是y轴(即直线x=0)

2.抛物线有一个顶点P，坐标为P( -b/2a，(4ac-b ^ 2)/4a)；当-b/2a=0时，p在y轴上；当δ = b 2-4ac = 0时，p在x轴上。

3.二次系数A决定了抛物线的张开方向和大小。

当a > 0时，抛物线向上张开；当a < 0时，抛物线向下打开。|a|越大，抛物线的开口越小。

4.第一项系数b和第二项系数a共同确定对称轴的位置。

当A和B符号相同(即AB > 0)时，对称轴在Y轴左侧；当A和B符号不同时(即AB < 0)，对称轴在Y轴的右侧。

5.常数项c决定了抛物线与Y轴的交点。

抛物线和y轴相交于(0，c)

6.抛物线与X轴的交点数量

当δ = b 2-4ac > 0时，抛物线与x轴有两个交点。

当δ = b 2-4ac = 0时，抛物线与x轴相交。

当δ = b 2-4ac < 0时，抛物线与x轴不相交。x的值是虚数(x =-b√b ^ 2-4ac，乘以虚数I，整个公式除以2a)

五、二次函数和一维二次方程

特别是二次函数(以下简称函数)y = ax ^ 2+bx+c，当y=0时，二次函数是关于x的一元二次方程(以下简称方程)，即ax ^ 2+bx+c = 0；此时函数图像与x轴是否有交点，即方程中是否有实数根。函数与x轴交点的横坐标是方程的根。

1.二次函数y = ax ^ 2，y = a (x-h) 2，y = a (x-h) 2+k，y = ax ^ 2+bx+c(在所有种类中，a≠0)具有相同的图像形状但位置不同。它们的顶点坐标和对称轴如下

解析式y = ax ^ 2，顶点坐标(0，0)，对称轴x = 0；

解析式y = a (x-h) 2，顶点坐标(h，0)，对称轴x = h；

解析式y = a (x-h) 2+k，顶点坐标(h，k)，对称轴x = h；

解析式y = ax ^ 2+bx+c，顶点坐标(-b/2a，[4ac-b ^ 2]/4a)，对称轴x =-b/2a；

当h >: 0时，将抛物线y = ax 2向右平行移动h个单位，即可得到y = a (x-h) 2的图像，

当h

当h >: 0，k >时；0，抛物线y = ax 2向右平行移动h个单位，再向上移动k个单位，就可以得到图像y = a (x-h) 2+k。

当h >: 0时，k & lt0，抛物线y = ax 2向右平行移动h个单位，再向下移动|k|个单位，得到图像y = a(x-h)2+k；

当h

当h

因此，通过研究抛物线y = ax ^ 2+bx+c(a≠0)的图像，将通式变为y = a (x-h) 2+k的形式，可以确定其顶点坐标和对称轴，从而明确抛物线的大致位置，为绘制图像提供了方便。

2.抛物线y = ax 2+bx+c (a ≠ 0)的图像:当a >: 0时，开口向上，当a

3.抛物线y = ax ^ 2+bx+c(a≠0)，如果a >: 0，当x ≤ -b/2a时，y随着x的增大而减小；当x ≥ -b/2a时，y随着x的增大而增大。如果a

4.抛物线y = ax ^ 2+bx+c的图像与坐标轴的交点:

(1)图像必须与y轴相交，交点坐标为(0，c)；

(2)当△ = b 2-4ac >时；0，图像与x轴相交于A(x1，0)和B(x2，0)两点，其中x1，x2为二次方程ax ^ 2+bx+c =

两个(a≠0)。距离AB=|x1-x2|

△ = 0时，图像与X轴只有一个交点。

△ : 0时，图像落在x轴上方，x为任意实数时，有y >:0；当一个

抛物线y = ax ^ 2+bx+c的最大值:如果a >:0(a & lt；0)，那么当x= -b/2a时，y = (4ac-b 2)/4a的最小(大)值。

顶点的横坐标是得到最大值时自变量的值，顶点的纵坐标是最大值。

6.用待定系数法求二次函数的解析表达式

(1)当给定的条件是已知图像经过三个已知点或已知x和y的三对对应值时，解析公式可以假设为一般形式:y = ax ^ 2+bx+c(a≠0)。

(2)当给定的条件是图像的顶点坐标或对称轴已知时，解析表达式可以设为顶点:y = a (x-h) 2+k (a ≠ 0)。

(3)当给定的条件是图像与X轴的两个交点坐标已知时，解析公式可以设置为两个公式:y=a(x-x？)(x-x？)(a≠0)。

7.二次函数知识很容易与其他知识整合，产生复杂的整合题目。所以基于二次函数知识的综合题是中考的热门题，往往以大题的形式出现。

反比例函数

y = k/x (k为常数，k≠0)的函数称为反比例函数。自变量x的取值范围是不等于0的所有实数。

反比例函数的镜像性质:反比例函数的镜像是双曲线。

因为反比例函数属于奇数函数，所以有f(-x)=-f(x)，图像关于原点对称。

此外，从反比例函数的解析公式可以得出结论，反比例函数图像中的任意一点都垂直于两个坐标轴，并且该点、两个垂直脚和原点所包围的矩形区域是一个固定值，这就是∣k∣.

当k > 0时，反比例函数图像通过第一和第三象限，并且是递减函数

当k < 0时，反比例函数图像经过两个或四个象限，为递增函数

反比例函数图像只能无限趋向坐标轴，不能与坐标轴相交。

知识点:

1.过反比例函数图像上的任意点作为两个坐标轴的纵剖面，这两个纵剖面和坐标轴围成的矩形面积为| k |。

2.对于双曲线y = k/x，如果在分母上加减任意实数(即y = k/(x m) m为常数)，相当于将双曲线图像向左或向右移动一个单位。(添加数字时向左平移，减去数字时向右平移)