求轨迹方程的常见方法，6种方法和3个注意事项

备战高考数学，每天积蓄力量

高中生数学学霸锻造“1天1道”行动

一、什么是轨迹方程？轨迹方程就是目标点的横纵坐标之间的一个等量关系。

二、求轨迹方程的常见方法：

由于动点运动规律所给出的条件千差万别，因此求动点轨迹方程的方法也多种多样。求轨迹方程的常见方法如下：

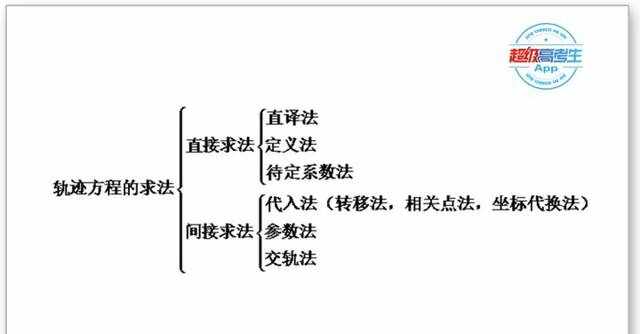
1．直译法：如果动点运动的条件就是一些几何量的等量关系，这些条件简单明确，易于表述成含x,y的等式，就得到轨迹方程，这种方法称之为直译法。用直接法求动点轨迹一般有建系,设点，列式，化简，证明五个步骤，最后的证明可以省略，但要注意“挖”与“补”。

2．定义法：运用解析几何中一些常用定义（例如圆锥曲线的定义），可从曲线定义出发直接写出轨迹方程，或从曲线定义出发建立关系式，从而求出轨迹方程。

3 . 待定系数法：若动点轨迹题意已直接告知，即为椭圆、双曲线、抛物线、圆或直线，则据题意直接用待定系数法求解。

4 . 代入法：动点所满足的条件不易表述或求出，但形成轨迹的动点P（x,y）却随另一动点Q(x',y')的运动而有规律的运动，且动点Q的轨迹为给定或容易求得，则可先将x',y'表示为x,y的式子，再代入Q的轨迹方程，然而整理得P的轨迹方程，代入法也称相关点法。

5 . 参数法：求轨迹方程有时很难直接找到动点的横坐标、纵坐标之间的关系，则可借助中间变量（参数），使x,y之间建立起联系，然而再从所求式子中消去参数，得出动点的轨迹方程。

6 . 交轨法：求两动曲线交点轨迹时，可由方程直接消去参数，例如求两动直线的交点时常用此法，也可以引入参数来建立这些动曲线的联系，然而消去参数得到轨迹方程。可以说是参数法的一种变种。

1．直译法：

【小编点评】此题就是题目中说什么我们就用什么，也不要转化，实实在在的送分题。不玩那些花式送分，送分就要实实在在同学们才喜欢。

2．定义法：

【小编点评】我知道大家看完肯定想吐槽没图是不是，我来给补上让你一分钟看懂上面的过程

是不是一分钟就看懂了，小编再说点跟大家相关的解题经验吧，小编比较喜欢做题，这题里面有两个点而且还关于原点对称，看到这里的时候我心里的想法就是百分之90的把握不是椭圆就是双曲线，接下来就只要去看看和为定值还是差为定值就可以了，建议大家作图做标准，因为这样你就不用想那么多了，图形中就能给你很多答案。

3.待定系数法

【小编点评】这个题是已知a的值，通过题目中的已知条件来求椭圆的方程，在小题里面这种技巧考的很多就是根据题目中的已知条件将椭圆上的点的坐标表示出来，之后代入到椭圆中求离心率e。

4.代入法：

【小编点评】代入法也叫相关点法，就是设要求的点的坐标为(x,y)之后根据题目中所给的条件中找到它与已知曲线上一点的关系，之后用x,y来表示已知曲线上的点的坐标，之后代入已知曲线就得到了x,y的关系，也就是轨迹方程。

5.参数法：

【小编点评】

6.交轨法：

三、总结：

1．直接法是基本方法；定义法要充分联想定义、灵活动用定义；代入法要设法找到关系式x’=f(x,y), y’=g(x,y);参数法要合理选取点参、角参、斜率参等参数并学会消参；交轨法要选择参数建立两曲线方程；几何法要挖掘几何属性、找到等量关系。

2．要注意求得轨迹方程的完备性和纯粹性。在最后的结果出来后，要注意挖去或补上一些点等。注：“曲线的方程与方程的曲线”的定义包括两个方面：一是曲线上点的坐标都是方程的解———称为纯粹性；二是以方程的解为坐标的点都在曲线上———称为完备性。两者缺一不可，否则就容易导致失误。

3．求轨迹方程一般只要求出方程即可，求轨迹却不仅要求出方程而且要说明轨迹是什么。

轨迹方程专题到这里就结束啦。

大家期待学习哪些专题内容可以在评论区给小编留言哈~也欢迎各种吐槽拍砖~

粉丝聚集地：微信公众号“1天1道”+ 官方QQ（125646959）—— 未来App专属社群