三门问题 著名的三门问题，是在 “胡扯” 吗？

上周，肖辉写了一部关于“三个问题”的漫画，这在他的朋友中引起了激烈的争论。没看过的小伙伴可以看看:

漫画:反直觉的“三问”

复习问题

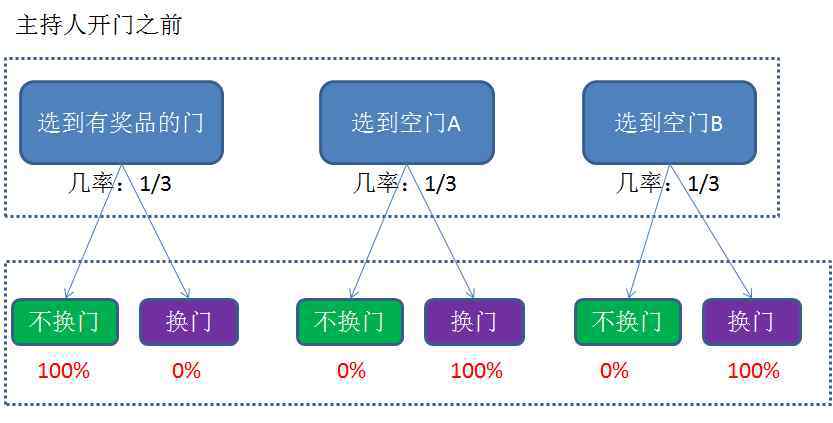
这道数学题来自一个娱乐节目。节目中有参与者，也有主持人。参赛者前方有三扇紧闭的门，其中空在两扇门后，另一扇门后是一辆法拉利跑车。

主持人知道哪个门后面有跑车，但参与者不知道。这时，让参与者选择一扇门。如果选择后面有跑车的门，跑车会作为奖励送给参与者。

问题一直很简单:有三门，参与者随机选择，获胜概率肯定是1/3。

以下是问题的重点。参与者做出选择后，暂时不打开这个门，然后主持人打开剩下的两扇门中的一扇门，也就是空门。

这时主持人给了参与者重新选择的机会:要么坚持刚才选择的门，要么换到另一个没有打开的门。

如果你是游戏参与者，如何选择赢取更多奖品？胜率多少？

这样的问题还需要问吗？有三门时，胜率为1/3；现在排除一门，剩下两门可以选一门，换门与否，胜率应该是50%。

然而，正确答案非常“违反直觉”:

换门胜率2/3

不换门胜率1/3

什么鬼东西？这简直不可思议！

在留言区，很多小伙伴提出了问题，很多人的想法和格雷自己的差不多:

“当最后还剩两扇门时，此时讨论的胜率应该是一个独立事件，应该与之前的参与者如何选择、主持人如何打开空门无关。既然是独立事件，那就选一个，胜率不是50%？

首先要明确一点，“换门”的胜率不是一个独立的事件，必须以第一选择为基础。在概率上，这种情况叫做条件概率。

那么，到底什么是独立事件呢？

举个例子，如果游戏的参与者原本是格雷，当格雷选了一扇门，主持人开了空门，不知真相的小红从外面跑了进来。小红不知道格雷选了哪扇门，只知道剩下的两扇紧闭的门中有一扇含有奖励。

这时候对于小红来说，无论选择哪一扇门，胜率都是50%，因为小红是在自主选择，而不是基于自己的第一选择“换门”。

这就是所谓的“独立事件”。

那么在“换门”的情况下，2/3的胜率是怎么来的呢？

在上周的漫画中，格雷用“贝叶斯理论”的思想来分析汇率和非汇率的胜率:

说白了就是把第一选择和第二选择的所有情况细化，分析每种情况下的条件概率，然后把这些概率相加得到最终结果:

不换门胜率=++= 1/3

换门胜率=++= 2/3

看了分析，有些朋友还是觉得不赞成。好吧，一定是格雷说得不够清楚。

所以这一次，让格雷从一个更加思考的角度来解释这个违反直觉的问题。

角度一:

假设没有主机帮忙开空门，换门和不换门的胜率分别是多少？

至此，换门也包括两种方法，但无论如何选择，胜率各占1/3:

主持人开门操作空换门胜率翻倍。为什么？因为换门的选项从两个减少到一个，准确率自然翻倍，从1/3到2/3；不换门的胜率还是固定在1/3:

角度2:

考虑一个更极端的例子，如果我们的游戏有10000个门，而不是3个门。

这时候你选门，胜率是万分之一。接下来，主持人为你打开9998门空。这个时候，你应该换门吗？

显然应该改。因为不换门的话，你的胜算很小，但是换门的话胜算高达9999/10000！

角度3:

还是回到三门的情况，第一次选一门的时候，你的胜算是1/3，这是毋庸置疑的。

如果此时给你一个“特殊选择”，让你要么坚持选择当前的门，要么打开除了刚刚选中的那扇门之外的所有门，只要其中任何一扇门有奖励，你就可以中奖。那么，你认为我们应该做出这个特殊的选择吗？

很明显，这个特殊选择的胜率是2/3，所以你一定要做出这个特殊选择。

在我们的问题中，主持人为你开了一个空门，留下你第一次选择的门和另一个关闭的门，给你换门的机会。

这种换门的选择，其实相当于刚才所说的“特殊选择”。

以上都只是理论分析，不妨用代码来实际测试一下。

public static void threeDoorsTest{//换门的获奖总次数int changeWinCount = 0;//不换门的获奖总次数int unChangeWinCount = 0;Random random = new Random;for{List<Integer> doors = new ArrayList);int bonusDoor = random.nextInt ;int selectedDoor = random.nextInt ;//主持人打开一扇空门for{if!=selectedDoor && doors.get!=bonusDoor){doors.remove;break;}}//获得换门的序号int changedDoor = doors.get;if{changedDoor = doors.get;}//如果不换门有奖，unChangeWinCount加1；如果换门有奖，changeWinCount加1if{unChangeWinCount ++;}else if{changeWinCount ++;}}System.out.println;System.out.println;}public static void main {threeDoorsTest;}

不换门获胜次数:327

换门奖数量:673

数据结果很明显，不换门的赢家比例约占1/3，换门的占2/3。

三门问题真的是一个很有趣的数学问题。在上个世纪的美国，当这个问题第一次被提出的时候，也有很多人质疑，包括老师、学者甚至数学家。后来经过多次实验，人们逐渐达成共识。

质疑精神值得鼓励。只有通过提问，才能进一步提高思维。对于格雷的漫画和文章，欢迎大家随时提出更多的意见和想法。

最后，让我们向玛丽莲·沃斯·莎凡特致敬，这位才华横溢、才华横溢的天才提出了“三个问题”。

安利看一看格雷创造的自由知识星球。

给予是对格雷最大的支持！