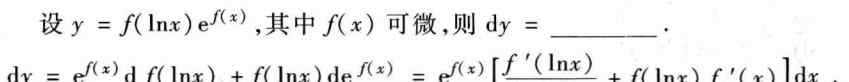前言
由于上限为O(NM) = O(VE)的SPFA算法的时间复杂度,卡死的概率非常高。在算法竞赛中,我们需要一个更稳定的算法:dijkstra。
什么是dijkstra?
Dijkstra是单源最短路径算法,时间复杂度上限为O(n ^ 2)(naive),在实际应用中相对稳定。堆优化后有O((n+m)log_{2}n的时间复杂度,在密集图中表现良好。
Dijkstra的原理/过程?
Dijkstra的本质是贪婪,只适用于没有负权边的图。
我们把点分为两类,一类是确定最短路径的点,称为“白点”,另一类是没有确定最短路径的点,称为“蓝点”
Dijkstra的流程如下:
1.初始化dis[start] = 0,其他节点的dis值为无穷大。
2.找一个dis值最小的蓝点X,把节点X变成白点。
遍历x的所有输出边(x,y,z),如果dis [y]>:用dis[x]+z,让dis[y] = dis[x]+z
4.重复步骤2和3,直到所有点都变成白色斑点。
时间复杂度为O (n 2)
为什么dijkstra是正确的
当所有边长都为非负时,全局最小值不能被其他节点更新。因此,在步骤2中找到的蓝点X必须满足dis[x]是从起点到X的最短路径,我们不断选择全局最小值进行标记和扩展,最终可以得到从起点到每个节点的最短路径长度
示意图
(make start = 1)
一开始,我们将dis[start]初始化为0,其他点初始化为inf
例子入门模板:P3371
高级模板:P4779
其他例子,请右转至洛谷题库,搜索“最短路径”
附笔
本文的一部分摘自李玉东的算法竞赛和信息学奥林匹克竞赛高级指南
友情提示:正权重图请使用dijkstra算法,负权重图请使用SPFA算法
感谢洛谷管理员提供的平台
这篇文章是小孙在《洛谷日报》上发表的
原地址:https://www.luogu.org/blog/61966/dijkstra
1.《dijkstra算法过程图解 [洛谷日报第31期]dijkstra详解》援引自互联网,旨在传递更多网络信息知识,仅代表作者本人观点,与本网站无关,侵删请联系页脚下方联系方式。
2.《dijkstra算法过程图解 [洛谷日报第31期]dijkstra详解》仅供读者参考,本网站未对该内容进行证实,对其原创性、真实性、完整性、及时性不作任何保证。
3.文章转载时请保留本站内容来源地址,https://www.lu-xu.com/yule/1019107.html