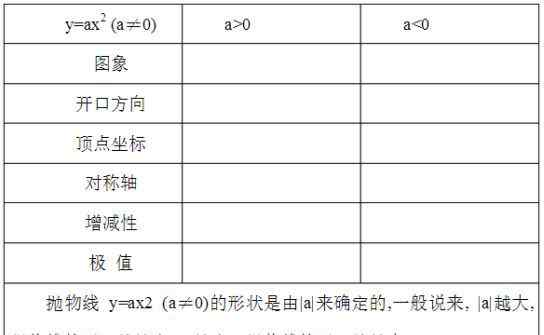
对于基本初等函数的导数，一定要熟悉。这是高中学的一个知识点。对于基本初等函数和复合函数的导数，关键是适当选取中间变量，将给定的初等函数分解成基本初等函数的复合或四次运算。复合函数求导时，首先要导出中间变量，自变量要乘以中间变量，这样每一步都是基本初等函数的求导。
(2)解:y ' =-sin(1+sin 1/x)*(1+sin 1/x)' = 1/x 2 * sin(1+sin 1/x)cos 1/x
注意：这个题目运用的是四则运算及复合函数的综合，题目不难，重要细心，也在考试时经常考，属于送分题；dy=.............dx，这里面的dx一定要写上，否则没分，往往我们很多考生都遗漏这一点，切记！注意:本主题使用四个操作和复合函数的合成。题目不难，重要，仔细，考试时经常考，属于分题型；Dy=.............dx，里面的dx一定要写下来，不然不会有分数，这是我们很多考生经常错过的。记住！
当x≠0时，由导数定律定义y' = 2/√ x * sinx+√ x * cosx，当x=0。
x→0，f '(0)= limf(x)-f(0)/x-0 = lim√x * sinx/x = 0(x→0)
注意:从y ' =(√ x * sinx)' = 2/√x * sinx+√x * cosx，公式在x=0点没有定义，得出f'(0)不存在，这无疑是错误的，因为√x在x=0点不可导，所以乘积的求导法则不适用。这也说明，即使不是分段函数，有时也需要用定义来推导，即使乘积中的某个因子在某一点不可导，乘积也可能在该点可导。如果你觉得边肖的理解和安排对你有帮助，不足之处还在意料之中，请关注，欢迎在这里评论，我会一直努力，加油。
1.《ln的运算法则 大学高等数学：第二章第三讲导数四则运算及复合函数微分法则》援引自互联网，旨在传递更多网络信息知识，仅代表作者本人观点，与本网站无关，侵删请联系页脚下方联系方式。
2.《ln的运算法则 大学高等数学：第二章第三讲导数四则运算及复合函数微分法则》仅供读者参考，本网站未对该内容进行证实，对其原创性、真实性、完整性、及时性不作任何保证。
3.文章转载时请保留本站内容来源地址，https://www.lu-xu.com/guonei/1017524.html
