幂函数图像 高一数学 ： 最全函数图像汇总，不看准后悔！

函数图像是高考必考的考点，对于研究函数的单调性和奇偶性，以及最大值和零点都有重要作用。但是很多同学看到眼花缭乱的分辨率功能，已经晕了。如果他们再画图像，不是这里不对就是有问题，图像画的乱七八糟，更别说用图像解决问题了！

绘制函数图像有几个步骤:

首先，观察它是否是一个基本初等函数。如果是，可以画；

如果没有，继续第二步，看看是否经历了一系列的函数变换，如:折叠变换、对称变换、伸缩变换、平移变换等。如果是，按照变换规则画一个图像。如果不是，基本上不需要单独画这个函数图像。那种题目基本会考查选择题，有四个选项可以选择！

下面我就整理一下基本初等函数的图像和函数变换的规律，希望大家可以学习一下！

一、图像的基本初等函数

1.第一个功能

性质:主函数图像为直线，当k >: 0时，函数单调递增；当k

2.二次函数

性质:二次函数像是抛物线，A决定函数像的开方向，判别式B ^ 2-4AC决定函数像与X轴的交点，对称轴两侧函数的单调性不同。

3.反比函数

性质:反比例函数图像是双曲的，当k >: 0时，图像经过第一和第三象限；当k

4.指数函数

当0

第二步:翻转变换得到函数y=ln|x的图像

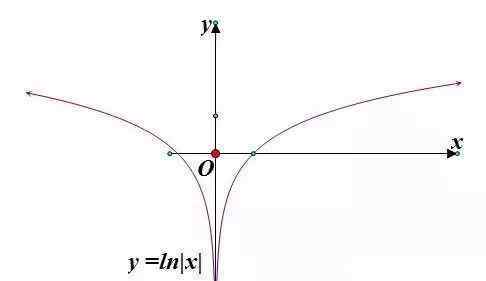
第三步:进行对称变换，得到函数y=ln|-x的图像

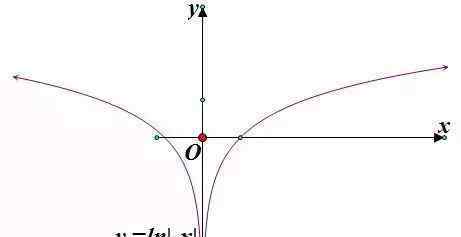
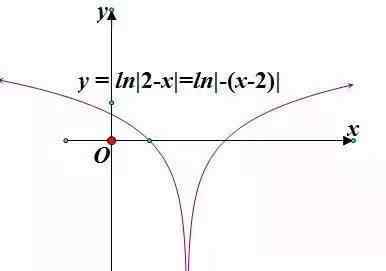
第四步:进行对称变换，得到函数y=ln|2-x的图像