黎奇 顾教授：第一性原理 - 与张首晟先生一席谈

美国科学院院士、中国海外院士、著名物理学家张首晟先生。

张首晟先生在美国中国科学技术协会第25届年会上发表了题为“科学、创新与投资”的演讲。

2017年10月初，美国中国科学技术协会第25届年会在纽约哥伦比亚大学举行。在会议上，老顾有幸再次见到了张唐毅夫妇和张首晟先生。张先生曾用杜甫的两句诗来形容自己:余馨一生最悲催，暮年更是山水甲天下。以前看到张先生的时候，总觉得他冷冰冰的，目光犀利。这次看到他，才发现他的脸很软，眼神很克制。偶尔一眼，眼睛突然蹿起来，摄人心魄。张太太依旧温雅。

会议组织者、美国科学技术协会副会长在机场迎接教授并宴请张教授时，对老顾说，他谈到了老顾。张教授对老顾写的一些文章很感兴趣。张教授原本是让严先生安排与教授和张先生共进午餐的。在颜老师的介绍下，张教授特意邀请了老顾一起吃午饭。(见《哈德逊河上的午餐》)。

近几年，老谷暑假经常在清华大学教计算共形几何，放学后经常在清华校园里随意闲逛，寻找数学方面的灵感，回忆青春的回忆。清华的教室走廊里，贴着清华系院士的画像和传记。其中一位是海外院士，温文尔雅，帅气自然。当你看着他的时候，脑海里突然出现了“玉面书生”这个人物。这就是张首晟先生，他离诺贝尔物理学奖只有一步之遥。老顾这次看到自己的偶像很激动。

张首晟先生在会上做了精彩的报告《科学、创新与投资》，回应了创新时代的呼唤，将优雅非凡的科学品味与睿智深远的投资眼光相结合，为喧嚣浮躁的科技投资界带来了一股清流。张首晟的主要原则是以简单驱动复杂，并追溯到真相，这是一个发人深省的事情。

张首晟接受了他下榻的川普国际酒店的采访。陪同他们的有中国科协美国佛罗里达分会的骨干姚远明教授和老顾前访法国里昂的弟子、现就职于Xi交通大学数学与统计学院的李慧斌教授。张先生学识渊博，涉猎领域广泛，对数学、金融、信息科学等诸多领域有着独特而深刻的见解。大家一起热烈讨论。

首要原则

凭借深厚的科学素养、敏锐的技术洞察力和非凡的市场远见，张首晟先生成功投资了VMWare，最高市值达到480亿美元。最近张先生在万丽公司创始人赛蒙斯先生的加持下，创办了丹华资本。赛蒙斯先生是先生的高足，陈-赛蒙斯的指示类已成为理论物理的基石之一。他创办的复兴公司几十年来一直是华尔街最赚钱的金融公司。他仇富，支撑着美国理论物理博士后生涯的一半。清华校园内，林故居“陈-赛门楼”附近有一座由赛门捐赠的雅致别墅。杨振宁和翁帆隐居在这里，写下了一个现代传奇。

张首晟先生优雅的投资品味和他坚定的科学价值观一脉相承，这就是第一原则。张先生认为，科学的最高志向是简单性和普遍性。张先生说:“我们生活的世界是复杂多变的，但如果我们能把一切都追溯到它的源头，我们就能以简单对抗复杂，赢得效率的提高。当我们理解并运用了第一个原则，就可以创新性地进行新联通，成为中心路由器。丹华资本也期望创业者从第一原则出发，思考问题。”

离散几何

老顾给张先生讲解了一些最近证明的数学定理，他的主要视野是在离散范畴中重构经典连续几何。这样做的目的一方面是为了适应计算机科学的发展，另一方面是为了从更直接、更基本的角度重新发现这些定理。经典几何需要流形的光滑结构，这样微积分的工具才能实现；计算机中的几何表示大多是离散的数据结构。基本的几何原理应该与光滑性无关，而是本质上更本质的规律。

比如经典的高斯-博纳定理揭示了一个曲面的全局曲率是拓扑不变的，证明了它需要二阶光滑性和相对现代的几何工具，比如动框架法。离散曲面的高斯-博纳定理证明只使用初等组合技巧。李慧斌的博士论文是关于几何近似理论，它建立了离散曲率和光滑曲率之间的关系。使用的理论工具是正态循环理论。在这个理论中，曲面嵌入在欧氏空和球面空的直积之间，在这个背景空中找到了特殊的微分形式，它在曲面上的积分给出了各种曲率测度。这样，我们将内在的高斯曲率外化，通过曲面嵌入的差异来控制曲率度量的差异。对于给定的光滑曲面，可以利用保角几何原理在曲面上均匀采样，然后建立测地线三角剖分，再用欧氏三角形替换每个测地线三角形，从而得到光滑曲面的离散逼近。随着采样密度的增加和三角剖分的细化，离散曲率测度收敛到光滑曲率测度。这样，我们用离散组合的方法证明了经典的高斯博纳定理。用这种思想，我们系统地证明了曲面微分几何的一些基本定理。

双曲线几何

欧几里得几何

球面几何

唯一性定理

根据张首晟先生的第一原理，曲面几何中最简单、最普遍的定理不是单值定理。各种复杂的曲面最终会共形地归结为三种标准几何之一，即球面几何、欧氏几何和双曲几何。这种简化复杂性，统一一切的理论，大大简化了纯理论的探索和实用几何算法的设计。埃舍尔的天使与魔鬼系列形象地刻画了单值定理。张首晟先生将最近发现的粒子命名为“天使粒子”，正是因为他读过汤姆·汉克斯的《天使与魔鬼》。

这种追求简单性和普适性的思想，是几何学中一贯的基本原理。三维流形上表面均匀化定理的推广是瑟斯顿几何定理。一个三维流形可以通过拓扑和运算分解为图元三流形，每个图元三流形允许八种几何之一。如果一个紧致闭三流形的所有圆都可以收缩到一个点，那么它就是一个三维球面拓扑的同胚，这就是著名的庞加莱猜想。

刘立淇

为了证明庞加莱猜想，汉密尔顿提出了里奇流的概念。Ricci流随时间演化出流形度量，度量的变换速率与当前Ricci曲率成正比，使得曲率变化满足某种非线性扩散反应方程。当系统达到平衡状态时，处处曲率不变。但在某些几何拓扑条件下，反应项占优势，曲率会在有限的时间内爆发。我们在爆发点将流形分成两部分，对每一部分应用Ricci流进行进一步变形。我们需要证明曲率爆破的次数是有限的。

与连续曲面黎曼流理论平行的离散曲面黎曼流理论已经完全建立并转化为一种强大的算法，在许多工程和医学领域发挥着重要作用。张先生告诉老顾，物理学家也做过类似的工作，并给出了具体的名字。同时，张先生也十分关注三维流形中离散黎曼流的进展。我向他解释了我们在双曲三重流形中所做的一些工作。几何定理的自动证明一直是数学家的梦想。

吴文俊先生对机器定理的证明

张先生讲了人工智能的发展，联结主义的神经网络进步很快；象征主义的机器定理证明也在稳步推进。吴文俊先生对机器定理的证明几乎可以证明所有的欧氏几何命题，而且经常给出奇怪而新颖的证明方法。但是计算机无法将冗长的证明分解成几何引理，使得人类很难理解计算机给出的证明。同时，到目前为止，计算机还没有发现人类尚未知道的非常深刻的基本定理。

吴先生发明的机器证明法的思想是这样的:我们用多项式表示条件，结论也用多项式表示。我们需要证明结论多项式包含在条件多项式生成的理想中。这可以用格罗布纳基法或吴法来验证。吴法忽略了根的多重性，所以更有效率。Grobner基方法给出完整的信息。希尔伯特定理保证了两种算法的收敛性:多项式环中的所有理想都是有限生成的。但是Grobner基方法的复杂度可以很高，解决一些问题的复杂度可以超过指数级。这种代数方法非常普遍，可以用来研究黎曼曲面的几何问题。

研究黎曼曲面的方法有很多。一种方法是利用几何分析建立几何偏微分方程求解；另一种是用代数曲线表示黎曼曲面，用代数几何研究。代数方法绝对准确，最后归结到判断理想成员的问题，所以计算复杂度很高。几何偏微分方程的方法可以适度逼近，因此更快速有效，在实践中得到广泛应用。然而，有许多几何问题只能用代数方法来回答，如连接分析和拓扑学的黎曼-罗赫定理。

费马最后定理

亏格为1的黎曼平面对应的代数曲线是椭圆曲线。当我们把椭圆曲线的域从复域变为有限域时，连续曲面就变成了离散点集，黎曼平面的一些几何性质就表现出数论性质。椭圆曲线是三次曲线，可以用一些函数来表示。如果参数表示的函数可以是模形式，我们称之为模曲线。顾山治村猜想所有的椭圆曲线都是模曲线，每个椭圆曲线对应一个模形式。如果费马定理不成立，我们可以构造一个椭圆曲线，它不是模曲线。所以孤山-志村猜想包含费马大定理。

1995年，怀尔斯证明了孤山-志村猜想和费马大定理的一部分。因为顾山无法证明自己的猜想，他在结婚后不久就在海里自杀了，一个星期后新娘也跟着去了，尴尬至极。模曲线在椭圆曲线的模空之间，模形式可视为模空之间的函数，与黎曼猜想有关。孤山之村定理是当今数学的核心问题——朗兰兹计划的特例。Langlands的程序使数论几何化，集代数几何、数论、群论于一体。

美国科学技术协会年会的热点之一是区块链。区块链的核心是用技术代替第三方担保，尤其是分布式存储技术和数据加密技术。数据加密的核心是数论。随着费马定理的征服，椭圆曲线加密技术蓬勃发展。黎曼猜想和量子计算的发展将极大地推动金融技术的发展。

伽罗瓦群论

说到群论，张首晟先生非常欣赏伽罗瓦的理论。为了解决高阶多项式方程根解的存在性问题，伽罗瓦亲手发明了群论。伽罗瓦认为，如果我们可以将一个N次多项式方程进行多步变换，每一步都变成一个变量的幂等于一个常数的形式，那么由N个元素排列而成的对称群就可以分解成一系列嵌套的子群，这样每两个相邻子群的商群就是一个循环群，即N次对称群就是一个可解群。因为五阶及更高阶的对称群不是可解群，所以五阶及更高阶的方程没有通式解。

伽罗瓦群论是每一个青少年成长过程中智力升华的关键环节。伽罗瓦群论所蕴含的审美价值和精神力量，在塑造青年人的价值观和人格方面，并不比唐诗宋词逊色。在法国，每个男孩成年后从母亲那里得到的礼物，往往是一份法国历史上著名数学家的手稿，就像中国父亲送给孩子的唐诗宋词选集一样。

比伯巴赫猜想

代数曲线是黎曼曲面的代数表示，是魏良周定理的特例。周定理证明了任意复解析流形在复投影空之间的全纯嵌入是代数的。研究黎曼曲面的另一种方法是复变函数理论。午餐时，张老师讲了比伯巴赫猜想，它有如下几何意义。我们研究从单位圆到复平面的保角映射。

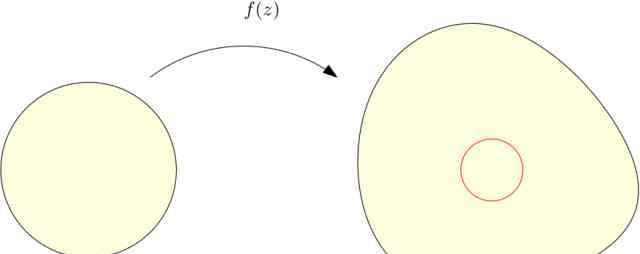
图2。保角映射的像集是复平面上的有界单连通区域。

这种保角映射可以用单叶解析函数表示。假设这个映射保持零点不变，零点处的导数为1，因此它具有级数表示:

,

Bieberbach猜测每个系数的模。

保角映射的像集是复平面上的简单连通区域，可以是有界区域，如图2所示；

图3。保角映射的像集是复平面上的有界单连通区域。

保角映射的像集是复平面上的简单连通区域，可以是无界区域，如图3所示。然而，Koebe1/4定理断言保角映射的像集包含一个半径为1/4的圆盘。

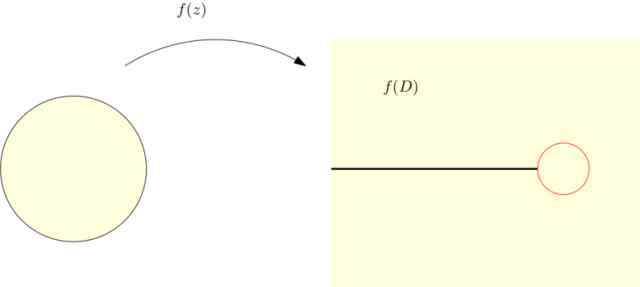
图4。Koebe映射。

在极端情况下，保角映射的像集覆盖整个复平面，其补是一组零测度，如曲线。该曲线尽可能延伸，直到触及Koebe1/4圆，如图4所示，此时映射幂级数的系数模也达到最大:

。

这是复分析几何理论中非常常见的神秘现象:几何极值包含解析极值。几何极值与解析极值的这种一致性可以用来证明许多保角变换的存在，如黎曼映射定理、狭缝映射定理等。

这再次证明了张首晟先生的简单而普遍的原则。

生成对抗网络GAN

近年来，人工智能的连接主义蓬勃发展。张首晟先生对此做了简要总结。“人工智能的爆发源于三个重要趋势的神奇融合:摩尔定律描述的计算能力的指数增长；互联网和物联网的爆炸式增长产生的海量数据；智能算法的快速发展。”张首晟先生赞赏对抗生成网络(GAN)原理:生成器试图生成欺骗鉴别器的样本，鉴别器试图识别真实数据并生成样本，两个神经网络同时训练，通过博弈相互提高，直到达到纳什均衡，鉴别器无法区分真实数据和生成数据，整个系统达到最优状态。

图5。甘模型生成人脸图像的结果。

图6。WGAN的框架。

这一阶段，丘成桐先生带领老顾和几位合作者从理论层面探索人工智能的计算模型。对抗生成网络可以用最优传输理论来解释。从统计视觉的观点出发，我们把所有nxn个图像组成的线性空空间定义为图像空空间(背景空空间，每个图像都是这个空空间中的一个点。我们考虑一个概念，比如人脸，所以每张图片都有一个概率来描述这张图片是否是人脸，所以我们定义一个概率分布。那么大部分图片都不是人脸，所以支持集是图像中的低维子流形空。

深度神经网络最成功的特点是可以将概念子流形映射到低维特征空，也称为潜在空间。特征空的维数远低于原始图像空当然深度神经网络也可以解码，解码图从特征空映射到图像空。

在特征空中，我们取一个标准的概率分布，如均匀分布或高斯分布。生成器构建解码图以将特征空之间的分布“向前推”到图像空之间的分布，该分布被记录为生成的分布。鉴别器深层网络计算数据分布和生成分布之间的距离。根据最佳传输理论，两种分布之间的差异可以通过所谓的瓦瑟斯坦距离来测量:

这里是所谓的c-变换，传递代价函数是例如从点到点传递单位质量的代价。

分布生成和替换后的最终优化问题可以简化为极大极小问题:

能量由鉴别器最大化，由发生器最小化，分别由两个深度网络承担。这两个网络交替训练，直到达到平衡。在这个模型中，它们是独立的，并且是单独优化的。

然而，经过深入研究，邱先生的团队发现了以下结论:

如果传输成本大于1，那么最优鉴别器和最优发生器之间有一个简单的数学关系，一个可以直接从另一个写下来。换句话说，我们只需要训练鉴别器和发生器中的一个，它们之间的交替训练是不必要的，它们之间的竞争实际上是虚构的。

计算最优传输相当于解凸几何中的闵可夫斯基问题和亚历山大洛夫问题，这两个问题用加斯帕尔·蒙日-安培方程描述。加斯帕尔·蒙日-安培方程在物理光学中具有明显的物理意义。

最优传输与几何上的Voronoi图/Delaunay三角剖分有着很深的内在联系。在计算几何中，功率图可以给出最优传输的几何解释:鉴别器相当于功率距离，发生器相当于功率图的单元分解，加斯帕尔·蒙日-安培方程的解相当于功率图的上包络，等等。

这些发现有助于更深入地理解GAN模型的本质，并有助于设计更严格和更有效的计算模型。

张首晟先生赞同用严格的理论来解释深度学习模式的分析方向，并鼓励老谷尽快将这些研究成果公之于众。这和他的第一原则密切相关。

时光飞逝，夜幕降临。我们同意张先生下次见面，在哥伦布圆环说再见。暮色中，曼哈顿的灯亮着，车水马龙，摩天大楼拔地而起，乌云滚滚空闪电若隐若现。老顾看着先生消失在曼哈顿的红尘里，像一个白衣侠客，武功绝世，儒雅灵动，没有幻影。一个量子拓扑，传唱于世；资本利剑杀人，投资江湖必然掀起血潮。。。