100以内的质数有 如何找出n 以内的全部素数

本数学教学研究微信官方账号内容均为邵雍本人原创，可转发，但转载需邵雍授权。每周推两三篇内容有分量的数学文章，但力求文笔简单。几分钟就能看完，轻松学数学。

本期讲的是素数，属于数论范畴，不过不用担心，我尽量简单说一下。相信你仔细看了就明白了。今天是周末。如果没有时间细读，可以先收藏起来，以后有时间再看。

如何求任意正整数n内的所有素数？例如，n等于100，300，1000，34567。

我们知道有一种所谓的“Elatosyny筛选法”，可以逐渐“筛选”出越来越多的素数。它的做法是:把所有从1到n的正整数按照从小到大的顺序排列，可以是一行一列，也可以是矩阵的形式。例如，如果n=157，我们将第一行排列成十个数字:1，2，3，4，5，6，7，8，9，10；在第二行，有十个数字11，12，...,20, ...，第15行填充前150个数字，然后第16行有7个数字151到157。我们以n=100为例，看看如何利用“Elatosyny筛选法”以最经济的方式找到100以内的所有素数。

“Elatosyny筛选法”具体操作步骤如下:第一步:删除第一个数字1。第二步:把目前还没有删除的数字中的第一个数字(最小的数字)圈起来，然后在圈起来的数字后面把这个数字的倍数全部删除(注意这里的删除通常会在上面划一个斜线)。其实第二步圈出来的数字是2，删除的数字是4，6，8，....第三步:类似于第二步的操作方式，具体来说，在目前还没有圈出或删除的数字中圈出最小的数字，然后删除大于3的3的倍数，即删除，9，15，...(注意有些3的倍数也是2的倍数，比如6，12等。，之前已经删除；当然，在6，12等上画一条对角线也不是没有道理，不影响我们的操作程序。如果你一直这样做，你可以找出100以内的所有素数。

那么，要做到这一点需要几个步骤呢？按说，步骤应该和元素一样多。现在不知道100以内的素数有多少，比如32，那么32步之后任务就够重了。那么，我们一定要走这么多步吗？答案是，不，我们根本不用走那么多步，我们可以少走很多步。具体取100平方根:√100(即根数100，注意表示如下)。我们取100的平方根的整数部分，也就是10(正好是10，但一般不一定是整数，然后取它的整数部分。比如n=101，那么101的平方根是10: 00，我们取其整数部分10)。所以我们的结论是，我们只需要进行“圈删除”的重复操作，直到所有不大于10的正整数都被圈起来或删除。具体来说，不大于√100的最大素数是7，所以可以对圈7进行“圈删”操作，删除7后的7的倍数。有4个素数(2，3，5，7)不大于10，也就是说，我们只需要做上述的“圈删”运算四次。这样，所有没有被删除的圆和数都是小于100的素数。如下图所示。倒计时，100以内有25个质数。

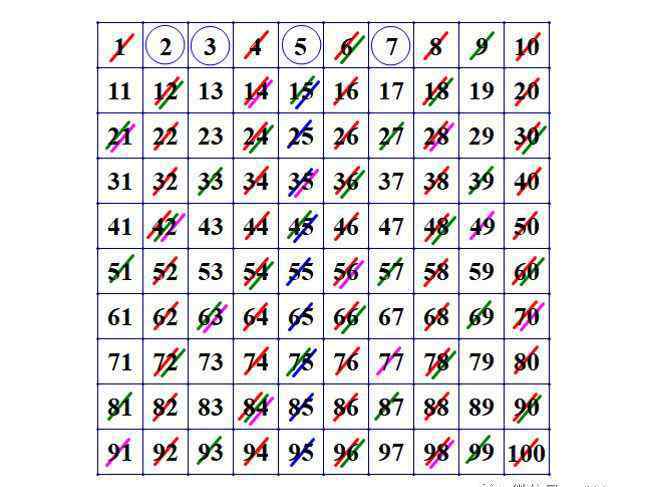
你可能会问，圈质数没问题，删非质数也没问题。但是经过四次“圈删”操作，还是有很多数字既没有圈也没有删。它们一定是质数吗？答案是:一定是质数！为什么？下面我来解释一下。请慢慢仔细阅读。

用反证法。因为经过以上四步，在√100(即10)内没有未关闭和未删除的数字，所有未关闭和未删除的数字都在√100到100之间。因此，我们假设在√100和100之间，这些未闭合和未删除的数中的一些是复合数(无论是素数还是复合数)。设这个数为p，那么√ 100

最后，我们证明了上述方法的可行性。其中√100很重要。虽然我们上面已经论证了n=100，但是这种巧妙的求素数的方法对于任意正整数n都是可行的，而且我们也可以用这种方法来判断任意正整数是否是素数:我们只需要求所有小于这个数平方根的素数即可。将这个数除以这些素数。如果它们都不能被整除，那么这个数就是质数。在这个过程中，求素数的方法就是前面介绍的“Elatosyny筛选法”。