说哲人哲人说 阿基里斯永远追不上乌龟与数学史上的第二次危机

芝诺 （约前490-前425），出生地为意大利半岛南部的埃利亚。著名古希腊数学家、哲学家，以其芝诺悖论而闻名于世。

芝诺

芝诺的二分法—在芝诺看来：“一个人从A点出发走到B点，要先走完总路程的1/2，再走完剩下总路程的1/2，再走完剩下的1/2……”如此循环往复，走完一个二分之一，还有下一个二分之一，所以在芝诺看来，运动是不可能的。

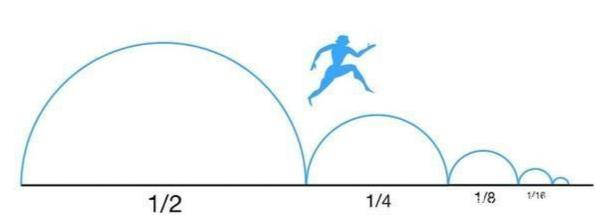二分法图示

而芝诺最为著名则是他的阿基里斯永远追不上乌龟的悖论，阿基里斯是古希腊神话中善跑者，但是却永远追不上速度比他慢十倍的乌龟，其悖论如下：

在阿基里斯和乌龟的竞赛中，阿基里斯的速度为乌龟的十倍，乌龟在前面先跑100米，阿基里斯在后面追，但他不可能追上乌龟。因为在他与乌龟的赛跑中，阿基里斯首先必须到达乌龟的出发点，当阿基里斯追到100米时，乌龟已经又向前爬了10米，于是，一个新的起点产生了；阿基里斯必须继续追，而当他追到乌龟爬的这10米时，乌龟又已经向前爬了1米，阿基里斯只能再追向那个1米，而当阿基里斯到达乌龟1米的位置时，乌龟由向前爬了10CM。于是，当阿基里斯到达乌龟第一个起点时，乌龟又创造了下一个起点，所以说，阿基里斯永远追不上乌龟。有没有感觉哪里不对劲，却又觉得他说的没毛病？

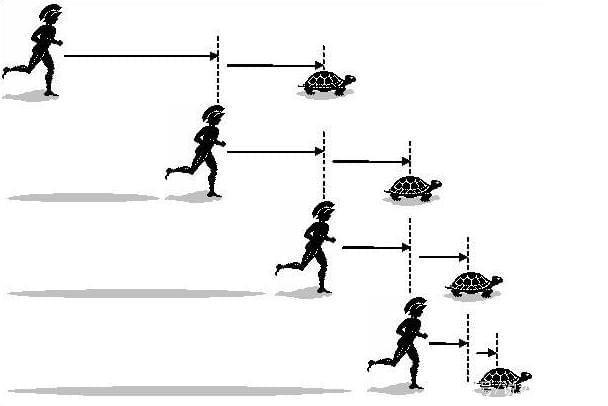阿基里斯与乌龟赛赛跑图示

我们知道，芝诺上面的悖论，只要是学过高等数学的人都可以解释为什么出现这样的悖论，这并是最早的微积分思想，芝诺认为1-0.999……=0,而1-0.999……大于0，但是芝诺初期的微积分思想却遭到他的师父巴门尼德的嘲笑，殊不知，这可以说是最早微积分的萌芽了。

对于以上两个悖论，我们知道阿基里斯的悖论明显错误，阿基里斯自己不知道吗？不，他知道，A点可以到达B点，同样，阿基里斯也肯定能追上乌龟，但是在当时的哲学界、数学界都认为芝诺这是明显的悖论，以至于在两千年以后围绕无限小问题——无限小是不是零的问题，无穷小及其分析是否合理？由此引发第二次数学危机，而微积分的出现，也使芝诺悖论问题得到正名。