平均数和中位数 数据分析中平均数其实并不准确，是时候开始使用中位数了

(a)法院

1906年，伟大的科学家、令人厌恶的种族改良倡导者高尔顿参加了一年一度的西英格兰牲畜展览会，并做了一个即兴的数学实验。

在集会上闲逛时，他遇到了一场猜拳比赛。人们猜一头公牛的重量，猜得最好的将赢得大奖。

高尔顿曾公开鄙视普通人的愚蠢。他认为只有专业人士才能做出准确的估计。787位嘉宾中专业人士很少。为了表示大众的无知，他计算了所有猜测的平均值(而不是当时统计学家常用的中位数):1197磅。当他得知实际体重时，他惊呆了:1198磅。

当今世界，我们只能看到平均数字:纽约4月份的平均气温是华氏52度；库里场均30分...只有在一些统计数据中(美国家庭年收入中位数为51，939美元)，中位数才会显示出来。

那么，中位数是怎么消失的呢？平均数是如何成为当今世界上最流行的量的？

(二)乙

俗称平均值，其实就是数学中的算术平均值，意思是所有数据的总和除以数据的个数。算术平均中的“mean”一词来源于拉丁语“medianus”。中庸的概念最早是由希腊数学家毕达哥拉斯提出的。

毕达哥拉斯时代的平均数不具有表征功能，它只指三个数中的数，而这三个数必须与两端的数有“相等关系”。这三个数字可以等距(如2、4、6)或相等(如1、10、100)。

统计学家丘吉尔·艾森哈特(Churchill Eisenhart)花了十年时间探索平均值和均值的起源，他说，与依赖大量数据进行计算的现代人不同，早期的科学测量非常不准确，科学家需要用理论来选择多个数据中最好的一个。

借助平均理论，古希腊天文学家托勒密从极少的观测中选择31'20作为月球的角直径。现在我们知道月球的角直径根据位置的不同从29'20到34'6不等。

在英语中，“平均”一词在1500年左右开始出现，指船舶或船上货物损坏造成的经济损失。如果由于船舶受损，船员不得不扔掉一些货物来减轻重量，投资者将使用算术平均法计算整体经济损失。渐渐地，这两个概念融合在了一起，这就是我们通常所说的平均。

许多年后，科学家将开始使用一个集中的量来表征一组数据。但不是平均数，也不是中位数，而是中位数。

(3).

科学工具通常是为了解决某些学科中的特定问题而创建的。在寻找集中量的过程中，人们想要解决的问题是用于导航的地理测量。

波斯学者比鲁尼。(masmoi)

比鲁尼是11世纪伟大的波斯知识分子，是已知的最早使用集中量的人之一。他试图测量古城加兹尼的经度。那时，当人们得到一组测量数据时，他们会去掉两端之间的数据，取最大值和最小值之间的算术平均值。我们今天称这个号码为中音。

艾森哈特发现17、18世纪仍盛行柱数。牛顿和其他航海家使用中间的柱数来计算地理位置。然而近几个世纪以来，在这个被平均占据的世界里，中层的数量已经流失。

(4).

19世纪初，算术平均成为一个常见的集中量。那个时代最杰出(也是最暴力)的数学家高斯在1809年写道:

如果你想在同样的情况下用同样的方法从几个直接观测值中选出一个数，这些数的算术平均值就是最接近真值的数。传统上，这个假设被认为是公理。

这到底是怎么发生的？

史书上没有明确记载。艾森哈特发现算术平均值可能是在地理大发现时代探索磁偏角(磁北与正北的夹角)的数学家第一次使用的。

直到16世纪后期，大多数科学家使用特定的算法来获得测量中的最佳值。但是在1580年，威廉·伯勒使用了一种新的算法来“组合”八个数据，声称磁偏角在11° 15 '和11° 20 '之间。虽然没有明确记录，但他可能用了算术平均。

1635年，英国天文学家亨利·盖勒布兰德称第一个已知的人使用平均值作为集中量。一天早上，他测得磁偏角为11°，那天下午，他测到了11° 32’。然后他写道:

“如果我们取算术平均值，我们可以确定正确的测量值是11 ^ 16’。"

这可能是人类用平均值来估计真相的第一步。

(5).

在数学中，中位数几乎与平均数同时出现。1599年，数学家爱德华·莱特首次推荐了记录中的中位数。

“许多箭射向一个标记，标记被去掉了。如果你想搞清楚标记原来的位置，也许可以想出这样的方法。他应该找到箭头最集中的地方:在这么多观察中，最中心的地方最接近真实值。”

在19世纪，中位数仍然是数据分析中不可或缺的一部分。在较小的数据集中计算中位数更容易。当时人们认为中位数比平均数更具有普遍性。

高尔顿也是中产阶级的坚定支持者之一。(维基媒体)

(6).

但由于平均数独特的统计性质及其与正态分布的关系，中位数在流行度上总是被平均数压制。

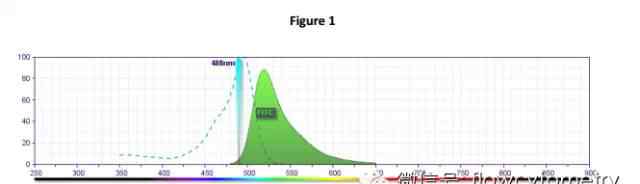
在很多情况下，大量的实测数据会呈现“正态分布”。人体身高、智商分数、年均气温等数据会以“钟形曲线”的形式分布，有高有低。

当数据正态分布时，平均值总是在钟形曲线的最高点，大部分数据会在中值旁边。通过标准差，我们还可以计算出距离平均值一定距离内的数据个数。

标准差，即数据中值与平均值之间距离的平方的平均值的平方根，使得平均值在分析实验数据和统计推断中具有突出的价值。没有这些特征的中位数在科学和统计学上逐渐失去了光彩。

计算机的出现也使得平均数更受欢迎。写一个计算平均值的计算机程序要比写一个计算中位数的程序容易得多。以至于在Excel中计算一些数据的中位数需要付出更多的努力。渐渐地，平均值被称为最知名，但不一定是最有代表性的值。

平均先生，中位数先生，Mode先生。(汉娜·霍尔特/灯泡书)

因为平均值容易受到极值的影响，所以在很多情况下，中值是帮助寻找配送中心的最佳值。许多分析师认为，使用平均值而不考虑黑白会损害我们对定量信息的理解。

回顾一下最近读到的平均房价和人均收入的数据，你会发现中位数是最能体现普遍性的代表值。最富有的1%可以极大地改变平均水平的位置。为此，美国人口普查局决定用中位数来衡量美国家庭的年收入。

平均也很难受脏数据的影响。由于统计人员需要处理越来越多的互联网数据，当工作人员遇到不准确的数据或打字时加一个零时，中位数就显示出其优越性。

(七)

随着数据收集和分析在我们日常生活中的重要性日益增加，我们需要重新检查用于表示这些数字的集中量。在理想情况下，分析师会同时使用平均值、中位数和众数，并用图像显示数据。

但我们生活在一个精力有限、时间短暂的社会。如果只能选一个数，就选中位数。

中位数和平均数的选择意义重大。通过选择平均值，心理学家很容易做出错误的诊断，金融家可能会误判市场的发展。平均统治了人类世界几百年。也许是我们做出一些改变的时候了。

煎蛋http://jandan.net/2016/05/06/average-mean-median.html