猜想 世界十大数学猜想及其证明情况

数据相关的数学与科学，算法与程序，资源与简化，机构与活动，政策与新闻，请关注DataSimplification Data Simp社区！~

微信官方账号id: chiefdataanalyst

为了使人类对自然或社会规律有一个可重复的共同认知，学术研究大多采用可观察、可测量、可验证的科学研究方法。科学研究就是观察和描述具体的自然和社会现象，用数学工具描述问题，形式化为严格的数学表达式，然后在科学理论中进行推论、证明、计算、推论、归纳和结论，找出其背后的规律。科研人员从宏观到微观进行科学思考，并对其进行加工，即分解观察、测量、表达、计算、证明的步骤，采用严格的数学工具对特定现象或问题的规律性解释或结论进行证明或证伪。如果研究者没有科学思维，只能泛泛而谈，用中国的意识形态理论(不是科学理论)去思考、讨论甚至写论文。

如果有人不相信数学简单，那是因为他们没有意识到生活有多复杂。——冯·诺依曼

目前，在自然社会中人类寻找规律的各种认知方法中，语言描述是最广泛的、随机的、不确定的，技术描述是最实用的，数学描述是最准确的、严格的、确定的。在不采用严格数学工具的研究范式的学术研究领域(非科研领域)，除了语言工具和技术工具之外，数学工具也有其应用，这里不做解释(详见“数据资源概述”和“数据简化技术”)。总之，数学工具在科学研究和学术研究中起着重要的作用。下面，我们从世界十大数学猜想及其证明中知道数学的魅力。

一、世界十大数学猜想(谜题)

世界十大数学猜想:NP完全问题、霍奇猜想、庞加莱猜想、黎曼假设、杨-米尔斯理论、纳维尔-斯托克方程、BSD猜想、费马大决策、四色问题、哥德巴赫猜想。其中，现代世界有三大数学问题:1。费马定理；2.哥德巴赫猜想；3.四色问题。世界七大数学题:1。p(多项式时间)对NP(不确定多项式时间)；2.霍奇猜想；3.庞加莱猜想；4.黎曼假设；5.杨-米尔斯' 6。纳维尔-斯托克斯方程的存在性与光滑性；7.伯奇和斯温纳顿-戴尔猜想。这十个数学猜想只证明了两个，庞加莱猜想和四色问题已经解决。

一、现代世界的三大数学问题

1.费马大定理

2.哥德巴赫猜想

3.四种颜色

二、世界七大数学难题

1.p(多项式时间)问题与NP(不确定多项式时间)问题

2.霍奇猜想

3.庞加莱猜想

4.黎曼假设

5.阳钢厂的存在与质量差距

6.纳维尔-斯托克斯方程的存在性与光滑性

7.伯奇和斯温纳顿-戴尔猜想

第三，要解决的数学问题

除了上面提到的著名的数学问题，还有下面几个著名的数学问题需要解决。

abc猜想

考拉猜想

周猜想(梅森素数分布猜想)

阿廷猜想(新梅森猜想)

哥德巴赫猜想

孪生素数猜想

克莱默猜想

哈迪-利特伍德第二猜想

六空之间的理论

我们先来看三个数学猜想(谜题)。

1.费马猜想

又称“费马大定理”或“费马问题”，由法国数学家费马于1637年提出。如果用不定方程表示，费马大定理是当整数n >: 2时，方程x+y=z关于x，y，z y，z没有正整数解。数学语言中，当n大于2时，x ^ n+y ^ n = z ^ n的方程没有正整数解。剑桥大学的Wiles在1995年彻底解决了这个大问题。

但在1到100的范围内，没有像27那样剧烈的波动(除了54等27的2次方的倍数)。验证游戏规则后发现，只有4k和3m+1(k，m为自然数)的数才能产生冰雹猜想中“树”的分叉。因此，在冰雹树中，16是第一个分叉，然后是64……每隔一段，产生一个新的支流。

自从康威发现了神奇的27，就有专家指出，27的个数必须只从54变，54必须从108变。因此，在27以上，必然存在一个不小于2n-33 * 2N (n = 1，2，3)的强大支流...)，但是，27到4-2-1系列和这个流2到4-1。按照机械唯物主义的观点，从27上游的数列群可以称为原点。但按照“下行直线”的观点，一般认为1-2-4-8 … 2n支路为“主流”。

等差数列验证法是基于海尔猜想验证规则的一种验证方法，处理的是无穷个等差数列的无穷个自然数。如果第一项是偶数，容差是偶数，那么序列上所有自然数都是偶数，所有序列都除以2。如果第一项是奇数，容差是偶数，那么序列上的所有自然数都是奇数，都乘以3再加1。如果容差是奇数，第一项是奇数，那么奇数项一定是奇数，然后乘以3再加1，偶数项一定是偶数，然后除以2。如果容差是奇数，第一项是偶数，那么奇数项一定是偶数，那么偶数项一定是奇数，除了2，所以乘以3再加1。按照这个计算规则，会遇到很多新的问题，考验验证者的智商。比如偶数的通式是2n，而且因为都是偶数，所以除以2得到n，n是自然数。

根据忽略偶数不记录的验证方法，第一个验证的奇数可以是可被3整除的奇数，也可以是不可被3整除的奇数。但是整个过程中达到并解析的第二个奇数和第三个奇数(如果存在)一定不能被3整除。如果都是由可被3整除的奇数来验证，那么路径上遇到的、到达的、访问的每一个奇数一定不能被3整除，但最终可以归结为1，那么所有奇数都必须遍历(遍历是离散数学的概念)。如果都是从不能被3整除的奇数来验证的，那么路径上遇到并归属的每一个奇数都不能再被3整除，最后归结为1(也就是说可以被3整除的缺失奇数不被验证)。因此，在正向冰雹猜想验证过程中，所有可被3整除的奇数都可以被命名为起点奇数，1是终点奇数，而在反向冰雹猜想验证过程中，情况正好相反，1是起点奇数，而可被3整除的奇数是终点奇数。其实在验证过程中，不能被3整除的奇数都存在于上一步无穷多个奇数中，占能被3整除的奇数的1/3，不能被3整除的奇数的2/3。这一现象与自然数的情况惊人地巧合。

又称角谷猜想，因为一个叫角谷的日本人把它传到了中国。

5.克拉特兹问题

角谷猜想也叫雪城猜想。其延伸之一是克拉茨问题，下面将简要讨论:

从20世纪50年代开始，这样一个奇怪而有趣的数学问题在国际数学界广为流行:如果任意给定一个自然数x，那么它是偶数的话就转化为x/2；如果是奇数，则转化为3x+1。此后，对获得的数继续上述变换。比如，如果x=52，那么可以依次得到26，13，40，20，10，5，16，8，4，2，1。如果你再做一次，你会得到一个循环:(4，2，1)。试试其他自然数，你会得到同样的结果。这就是所谓的锡拉丘兹猜想。

上述转换实际上是以下函数的迭代

{x/2 (x是偶数)

C(x)=3x+1 (x为奇数)}

问题是，如果从任意自然数出发，迭代有限函数c，最后能得到循环(4，2，1)，或者等价地得到1吗？据说克拉特兹在1950年举行的一次国际数学家大会上谈到了这个问题，所以很多人称之为克拉特兹问题。但是，很多人都是独立发现了同样的问题。所以从那以后，为了避免对问题归属的争议，很多文献都称之为3x+1问题。

奖励和解决方案

克拉特兹问题的吸引力在于，一旦在C的迭代过程中出现2的幂，问题就迎刃而解了，有无穷多个2的幂。人们认为，只要迭代过程持续足够长的时间，问题就会得到积极的解决。正是这种信念，在各地引发了“3x+1问题”热潮，大学和研究机构都不同程度地卷入了这个问题。许多数学家开始提供奖励，大约500美元和1000英镑。

数学题

日本东京大学的Mishida测试过240这个自然数，不到1.1万亿。1992年，G.T .莱文和M .维穆伦测试了自然数5.6*1013，没有发现反例。问题的意义是如此的清晰、清晰、简单，连小学生都看得懂。然而，对于20世纪的许多伟大数学家来说，这是困难的。当著名学者R.K.Guy介绍这个世界问题时，他甚至题为“不要试图解决这些问题”。经过几十年的探索和研究，人们似乎接受了大数学家P .鄂尔多斯的说法:“数学还没有成熟到可以解决这样的问题！”有人提出3x+1问题是下一个费马问题。

初步研究

以下是我对克拉特兹问题的初步研究结果，但是我发现了一个小规律，这个规律还远远没有解决。

克拉特兹命题:设n∈N，f(n)= n/2(如果N为偶数)或3n+1(如果N为奇数)

目前f1(n)表示f (n)，F2 (n) = f (f (n))，...fk (n) = f (f(...f (n)...)).

有一个有限正整数m∈N，这样fm(n)=1。(以下，n/2称为偶变换，3n+1称为奇变换，偶变换称为全变换)

6.蜂巢猜想

4世纪，古希腊数学家佩波斯指出，人们看到的六边形横截面的蜂巢是蜜蜂用最少量的蜂蜡建造的。他的猜想叫做蜂巢猜想。匈牙利数学家陶巧妙地证明了在所有首尾相连的正多边形中，正六边形的周长是最小的，但没有证明多边形的边是曲线的情况；当黑尔认为周长是曲线时，无论曲线是外凸还是内凹，他都证明了由许多正六边形组成的图形的周长是最小的。

你有什么样的数学猜想？继续找！

二.世界十大数学问题，奖励数百万美元的解决方案

10.纳维尔-斯托克方程的存在性与光滑性:小船穿梭于起伏的湖面，湍流的气流跟随我们现代喷气式飞机的飞行。无论是微风还是湍流，都可以通过求解纳维尔-斯托克斯方程来解释和语言。

9.杨-米尔斯存在与质量差距:杨-米尔斯理论是现代规范场理论的基础，也是20世纪下半叶的重要物理突破，旨在利用非阿贝尔李群描述基本粒子的行为，该理论由物理学家杨振宁和米尔斯于1954年首次提出。这一理论在当时不受物理学重视，通过1960-1970年间许多学者引入的对称性自发破缺和渐近自由的概念，发展成为今天的标准模型。

8.贝尔和斯维内顿-戴尔猜想:贝尔和斯维内顿-戴尔猜想认为有理点群的大小和点s=1附近的一个相关Zeta函数z(s)的行为是特别有趣的猜想。如果z(1)等于0，则有无穷多个有理点，如果不等于0，则只有有限个这样的点。

7.四色定理:四色定理的本质是二维平面的固有性质，即两个直线不相交，在平面上没有公共点。很多人已经证明，在二维平面上不可能构造出5个或5个以上的成对连通区域，但是还没有上升到逻辑关系和二维固有属性的层面，导致了很多虚假反例。然而，这些恰恰是对图论严密性的考证和发展促进。虽然计算机证明自己做出了数十亿次的判断，但只是在巨大的数量优势上取得了成功，这并不符合数学严格的逻辑体系。到目前为止，无数的数学爱好者都致力于这项研究。

6.哥德巴赫猜想:哥德巴赫在1742年写给欧拉的信中提出如下猜想:任何大于2的偶数都可以写成两个素数之和。但哥德巴赫本人无法证明，于是写了一封信请著名数学家欧拉帮忙证明，但欧拉直到去世也无法证明。1966年，陈景润证明了“1+2”成立，即“任何足够大的偶数都可以表示为两个素数之和，或者一个素数和一个半素数之和”。

5.费马定理:由17世纪法国数学家皮耶·德·费玛提出。它断言，当整数n >: 2时，关于x，y和z的x^n+y^n = z^n方程没有正整数解。它提出后经历了许多人的猜想和辩证，经过300多年的历史，终于在1995年被英国数学家安德鲁·怀尔斯彻底证明。

4.黎曼假设:黎曼假设是方程z(s)=0的所有有意义的解都在一条直线上，这一点被多次证明为围绕素数分布的许多谜团带来了曙光。伪素数和素数的通式告诉我们，素数和伪素数是由其变量集决定的。所以她的假设是错误的。

3.霍奇猜想:他猜想对于所谓的射影代数族，也就是空之间特别完美的类型，称为霍奇闭链的分量实际上是称为代数闭链的几何分量的(有理线性)组合。

2.庞加莱猜想:庞加莱猜想是法国数学家庞加莱提出的猜想。2006年，数学界终于证实了佩雷尔曼的证明解决了庞加莱猜想。庞加莱猜想是拓扑学中的一个基本命题，它将有助于人类更好地研究3D 空，其结果将加深人们对流形性质的理解。

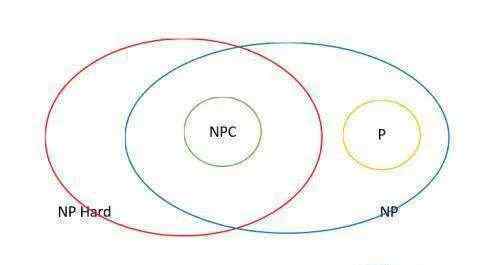
1.NP完全问题:如果一个人告诉你，你的数字13717421可以写成两个更小的数的乘积，他告诉你，可以分解成3607乘以3803，计算机验证。人们怀疑是在多项式时间直接计算还是找到正确答案。这就是NP=P？你猜，如果没有提示，要花很多时间才能解决。

(注:引用的相关资料[1-4]版权归原作者所有。)

材料(862k字)

1.lgy0104235，世界十大数学猜想是什么？[EB/ol]，百度，https://zhidao.baidu.com/question/327885132.html, 2011-10-09，访问日期:2019-08-12周一

2.郝南侃数学。著名数学猜猜你知道什么。[EB/OL]，百度，https://baijiahao.baidu.com/s? Id = 1606134329941476690，发布于18-07-1616: 52，访问日期:2019年8月12日

3.蓝海摄影。世界十大数学难题据说获得了数百万美元的奖励来解决。你认识几个？。[EB/OL]，https://百家号. baidu.com/s？Id=1603150608978784426，发表于18-06-1317: 53，访问日期:2019年8月12日

4.萤火虫沙龙，来自:莒县小屋>；抽象本质。你知道多少世界闻名的数学猜想？。[EB/ol]，http://www.360doc.com/content/16/0725/17/9771186 _ 578309578 . shtml，2016-07-25，2016-07-21，访问日期:。

X.秦隆基。西方哲学和人工智能，计算机；人工智能编年史；人工智能达特茅斯夏季研究项目建议书(1955年8月31日)；人工智能的研究现状及教育应用；计算机操作系统的演变、谱系和产品发展史；数据科学与大数据技术导论；数据资源介绍；追踪和简化文本数据；大数据简化技术体系；数据简化社区概述。[EB/OL]，数据简化DataSimp(微信微信官方账号)，https://dsc.datasimp.org/,http://www.datasimp.org, 2017-06-06。

—结束—

声明:已出版的期刊媒体资料的编纂仅用于学术新闻信息的传播，表明素材来源可以追溯。这个微信官方账号不持有任何倾向性，也不认可他的观点或言论。

世界十大数学猜想及其证明(10k字)

隆庆2010-2019年期间数据简化数据单

数据简化数据简单介绍:世界十大数学猜想及其证明。世界十大数学猜想:NP完全问题、霍奇猜想、庞加莱猜想、黎曼假设、杨-米尔斯理论、纳维尔-斯托克方程、BSD猜想、费马大决策、四色问题、哥德巴赫猜想。其中，现代世界有三大数学问题:1。费马定理；2.哥德巴赫猜想；3.四色问题。世界七大数学题:1。p(多项式时间)对NP(不确定多项式时间)；2.霍奇猜想；3.庞加莱猜想；4.黎曼假设；5.杨-米尔斯' 6。纳维尔-斯托克斯方程的存在性与光滑性；7.伯奇和斯温纳顿-戴尔猜想。关键词:数学，数学猜想，理论，概念。分享或感谢支持后，发送公众号对话框中的“数学猜想”，下载本文的PDF数据。

世界十大数学猜想及其证明(10k字)

目录

a世界十大数学猜想及其证明(8k字)

一、世界十大数学猜想(谜题)

二.世界十大数学问题，奖励数百万美元的解决方案

材料(862k字)

a世界十大数学猜想及其证明(8k字)

世界十大数学猜想及其证明

正文|秦长周期，数据简化数据simp 20190812 mon 0810 sat

世界十大数学猜想及其证明

简介:世界十大数学猜想及其证明。作者:秦隆基。资料:Web，新媒体，微信群聊资料，有引用来源。下载:如果需要本文10k字、18位数字、12页的PDF数据，分享或感谢支持后，官方号会发“数学猜想”获取链接。版权:科普文章仅供学习。一些出版资料的版权属于原作者。不要将它们用于非法商业目的。数据简化社区保留相应的版权。给QinDragon2010@qq.com留言或发帖。转载:请保留作者、来源、时间等信息，如“来自官方数据简化DataSimp，作者:秦隆基，时间:20190812Mon数据简化SataSmip社区NC非商业授权”等字样。

“数据简化数据简化”公共科技共享

社区:“数据简化数据简化，科学科学，知识简化”新媒体汇聚专业领域一线研究者；在学习技术的同时，我们也从专业的角度传播知识，解释和普及科学现象和原理，展示自然社会生活的科学方面。PhDS01由秦隆基发起，期待您在各个领域的参与；科技论文投稿邮箱DataSimp@126.com。只会敲门喊，不能推广领域；只有空想设计，却实现不了生产，他会浪费一生。工程技术能力很重要，秦隆基和君共享。欢迎来自科学、工程、技术、教育和媒体的专家投稿并加入数据简化社区！欢迎分享，欣赏，支持科普~ ~

如果您需要下载PDF，请感谢您的支持