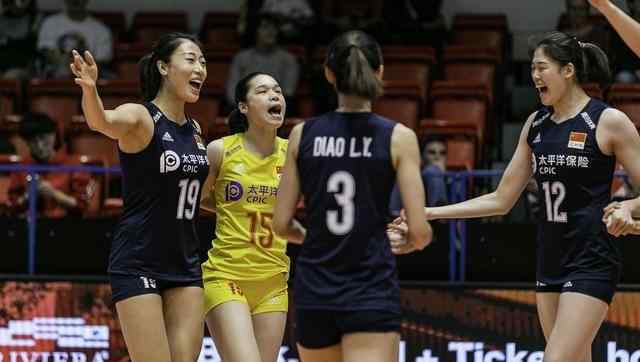在巅峰时期,被称为自助餐中的劳斯莱斯的美洲豹现在面临着历史上最大的危机。7月9日,证券日报记者来到翠微广场五楼的豹店。与对面酒店人围坐在桌边吃饭的场景相比,豹...
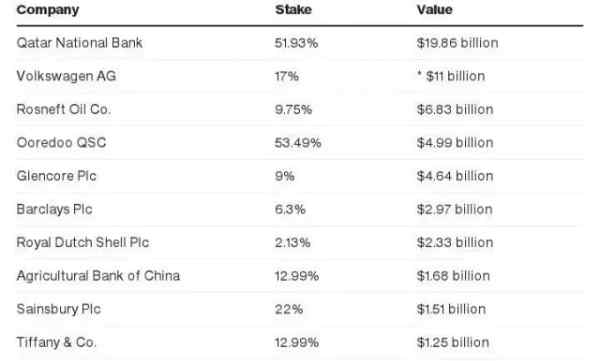
外交形势的突变给卡塔尔投资背景的奢侈品牌带来了更多的不确定性。昨天巴林突然宣布与卡塔尔断交,随后沙特、埃及、阿联酋、利比亚等中东国家也在同一天宣布与卡塔...
《想象欧洲》系列是一本篇幅很短的袖珍本。对于坐公交车上班的人来说,看书携带特别方便。按照正常的阅读速度,一天可以在上下班的路上看完一本书。黄金时代的西班牙...
林恺俊质疑项目的公平性,并炮轰对手和项目组。围棋手柯凯君表示,“退出这个舞台是对节目公平性最有力的抗争”。最受关注的选手“水格”王皓因为对手被怀疑作弊。愤...
加拿大的住房危机。加拿大温哥华繁华的房地产,最近一片荒芜,居民陆续搬走,留下的是废弃的“高端住宅”和惨淡的氛围。随着国际投资推高房价,温哥华的中产阶级已经无法...


无理数的发现——第一次数学危机
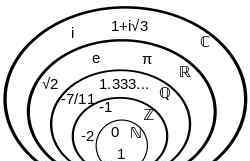
大约在公元前5世纪,不可通约性的发现导致了毕达哥拉斯悖论。当时的毕达哥拉斯学派非常重视对自然界和社会中不变因素的研究,把几何、算术、天文、音乐称为“四大艺术”,在其中追求宇宙的和谐规律性。他们认为宇宙中的一切都可以归结为整数或整数之比,毕达哥拉斯学派证明了毕达哥拉斯定理,但也发现有些直角三角形的斜边不能表示为整数或整数之比(不可公度性),比如直角都是1的直角三角形。这种悖论直接违背了毕学派的根本信条,导致了当时认知的“危机”,从而导致了第一次数学危机。

公元前370年,比西学派的欧多克索斯通过给比例一个新的定义解决了这个矛盾。他处理不可公度量的方法出现在欧几里得的《元素》第五卷。欧多克索斯和戴德金德1872年对无理数的解释与现代解释基本一致。中学几何教材中对相似三角形的处理仍然反映出不可通约性带来的一些困难和微妙之处。第一次数学危机对古希腊的数学观点产生了巨大的影响。这说明几何的一些真理与算术无关,几何量不能完全用整数及其比值来表示,而是可以用几何量来表示。整数的权威地位开始动摇,而几何的同一性上升。危机也说明,直觉和经验不一定可靠,但推理证明是可靠的。从此,希腊人开始重视解释和推理,从而建立了几何公理体系,这是数学思想的一次伟大革命!
无穷大是零吗?第二次数学危机
18世纪,微分法和积分法在生产和实践中得到了广泛而成功的应用,大多数数学家对这一理论的可靠性毫不怀疑。
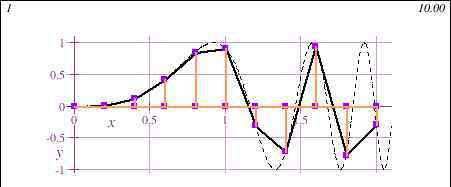
1734年,英国哲学家兼大主教贝克勒出版了《一个不相信正统的数学家的分析师或降临节》,指出微积分的基础——无穷小问题,提出了所谓的贝克勒悖论。他指出:“牛顿在求xn的导数时,首先给X一个0的增量,应用二项式(x+0)n,从中减去xn得到增量,再除以0得到xn的增量与X的增量之比,然后让0消失,从而得到最终的增量比。这里牛顿已经办理了违反矛盾律的手续——假设X有增量,增量为零,即假设X没有增量。”他认为无穷小dx既等于零又不等于零,被人叫着挥之不去是荒谬的。“dx是失去数量的灵魂”。无穷小到底是不是零?无穷小及其分析是否合理?这在数学乃至哲学领域引起了一个半世纪的争议。导致了数学史上的第二次数学危机。

如今我们的 GDP 已经全球第二,但是看技术革新和基础研究的创新能力,作为一个国家我们排在 20名开外。有的人或许会怀疑,认为我说的不对,会说我们都上天揽月、下海捉鳖...
今天下午,沈腾发了一条微博表示自己要将乔杉作为自己的明灯和榜样,原因竟然是因为乔杉的脸比小脸女演员的脸还要小,这个理由真是让人哭笑不得。不看不知道,一看吓一跳...
2021年,曾经的浙江巨富、电视剧《鸡毛升天》原型周晓光,面临着日益严重的危机。作为周晓光的核心资产,上市公司广信源成面临着退市危机。目前其最新股价仅为0.87元,已...
看到上面这张上世纪的海报,有没有一种时空穿越的感觉。糟糕的是,现在已经进入21世纪了,那帮90后的正在践行上世纪的海报精神!——“坚持晚婚晚育,甚至不育,把青春献给时...
浮世绘星座(微信号:新座168)覆盖各个星座控制 星座解密|财富分析|让爱情可预测 故事背景:由于某种不可抗力,十二星座被困在一个孤岛上。 他们是白羊座、金牛座、...
在很多人眼里不值一提的垃圾回收行业,曾经让很多人变得富有。但是这几年已经失去了以前的光环,行业不景气,各种废品价格涨跌,曾经随处可见的废品收购者慢慢消失。 最...
或许你还在为新冠病毒迟迟无法被消灭而担忧,但事实上人类还在面临着更加让人震撼的危机。人类每年排入大海的塑料废物达到了800万吨。截止到目前,海洋中充斥着至少5...